综合奖惩联合规则

五、综合奖惩联合规则

经过计算得到每位医师的奖赏值和惩罚值，需要进行最终的奖惩聚合得到医师绩效评价结果。本研究梳理了传统的决策理论，基于多种典型决策方法内置价值函数的对比分析（如与之思想一致的对立分值的联立、级别高于关系体系中的采用进流减出流、距离理想解评价模式的TOPSIS 采用相对比率法等多种不同形式），系统研究了决策理论具有的内置价值函数。而到目前为止，价值函数的研究一直是决策理论中被忽视的方面。并且，本研究将决策者的行为倾向纳入综合奖惩联合价值函数的研究，通过设置行为参数以适应行为经济学中的损失厌恶概念。决策者可以在不同决策情景中灵活设置损失规律比率以反映其在不同情景下的选择倾向。

由于医师绩效的奖赏值和惩罚值呈现相反的目标，即决策中想要最大化Ri并且最小化Pi，因此本研究可以提出一个简单的价值函数：

情形1：

该类模型是最常见模型。通过将奖赏值减去惩罚值，得到最终的绩效评价结果，评价结果介于-1 到1 之间。该方法操作简单，易于理解，得到的结果可以很好地反映医师是被奖赏还有被惩罚的。

而现实生活中，由于禀赋效应人们普遍厌恶损失。具体来说，失去与得到同样的东西相比，损失的痛苦感知大致是快乐感知的两倍。这意味着只有当获得两个单位的收益时，决策者才愿意承担放弃一个单位的损失。但也有研究者指出，决策者的风险态度受决策情景及参照物的影响，它们的变动会引起决策者风险态度的转变。为此，本文试图将决策者的风险态度体现在价值函数中。基于此，本文对式（5-24）价值函数进行了改进，具体见下式：

其中：1≥ λ≥0 。λ 表示奖惩之间权重，则是决策者的损失厌恶率。过将奖赏值和惩罚值之间设立权重，可以更加灵活的刻画决策者在不同决策态势下的风险态度。在不同决策情景下，评价者通过设立不同权重λ 以体现自身态度倾向，并基于此获得不同倾向下的医师绩效评价结果。

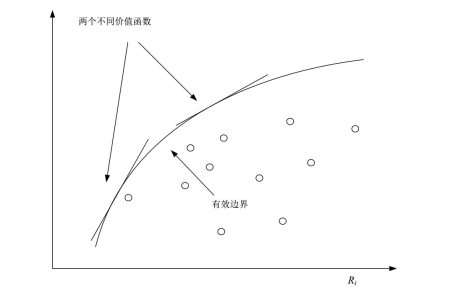
图5-3　不同损失厌恶率下的选择

情形2：

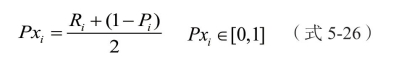
该类模型趋向于对医师的奖赏。由于 Pi 必然小于0，所以1-Pi 必然大于0，所以此模型可以看作是医师两种奖励的加权平均，一种为计算得到的奖赏值，另一种是得到较少惩罚值而获得的奖赏，最终的计算结果也是介于0 和1 之间。该模型适合于对所有医师展开奖励时使用，因为结果全部为正，可按照计算结果直接对医师展开相应奖赏，但也会有一定的局限性。由于结果全部为正，仅凭一个人的绩效评价结果无法反映该医师在所有医师中处于表现较优还是表现较差。

情形3：

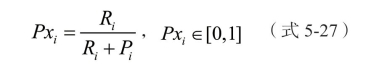
该类模型趋向于对医师的奖赏，可看作为类似于情形2 的另一种计算方式。这两种计算方式却略有不同，为了解这两种计算方式的不同，模型不同的奖惩数值，观察其趋势演化。奖赏值最小值设为0.01，最大值设为1，中间每隔0.01 取一个数，这样共取得100 组奖赏值，同样的方式取惩罚值，获得100 组惩罚值。而两者组合，获得10000 组奖惩数据，计算两种计算方式下的最终结果。情形2 的绩效评价趋势如下：

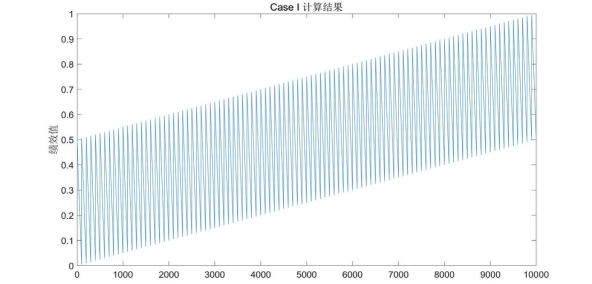
图5-4　情形2 的绩效评价趋势

情形3 的绩效评价趋势如下：

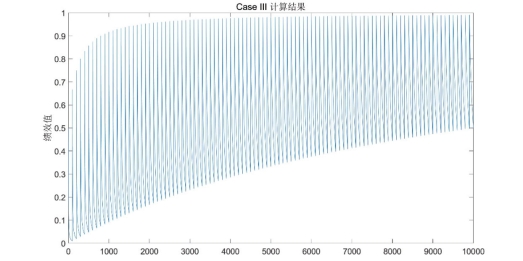
图5-5　情形3 的绩效评价趋势

由这两张图可以看出，情形 3 的计算方法比情形 2 的计算方法波动性更大，即情形 3 计算方法最终获得的绩效数据更加分散，而情形2 计算方法获得的绩效数据更加集中。评价者可根据实际情况选择适合的方法去计算医师绩效。

情形4：

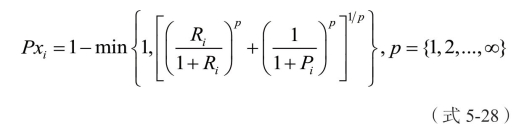
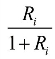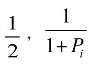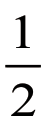Pxi∈[0，1] 此方法是一种惩罚倾向的绩效评价方案。并且，的数值介于0 到的数值介于到1。

首先分析最简单的一种情况，当 p=1 时，考虑一种最优的情况，即 Ri=1，Pi=0，则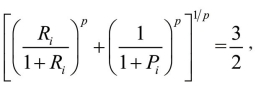Pxi =0。最差情况，即 Ri=0，Pi=1时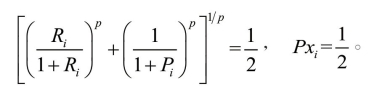，即最优惩罚值为0，最差惩罚值为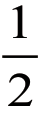。而当 p=2时，当最优时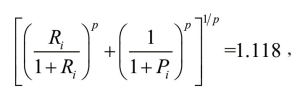，最终结果为0。当最差时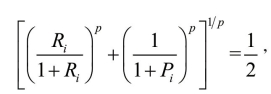，最终结果为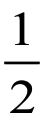 。随着p 的增加，数据越来越集中，而p 的存在，使该模型中奖惩的实施更加灵活。

上述提供了4 种奖惩聚合方法，对不同之处已进行了详细描述。在实际中，可根据评价者态度和评选态势的变化灵活选择不同方案对医师绩效展开评价。