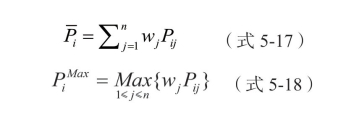基于幂式范数的医师绩效指标间的平衡聚合规则
基于上文得到各位医师在不同指标下的奖赏值和惩罚值，关于其指标聚合方式选择将在本节重点探讨。在医师绩效考核这项系统性工作中，多指标聚合并非是在完全补偿与不补偿间之间简单调和，而还应深层次的考虑多指标共同作用的协同效应及其对考核系统的整体影响。基于文献[130]等研究，本文提出基于幂式范数的医师绩效指标间的平衡聚合规则。该聚合规则通过闵式范数不同取值体现对评价问题指标间冲突的妥协，即指标间的不同补偿程度。具体的，指标奖赏值的计算公式如下：
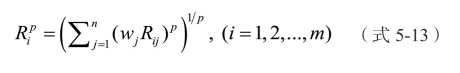
其中p∈ [1，∞），w j∈[0，1]且
不难看出其关键在于恰当地选择参数p 值，特别地，当p =1时，式（5-13）具体化为
，即为熟知的加权算术平均，其特点在于所有指标完全补偿，也就是说，表现较差的指标可由较好的指标补偿。当p →∞时，式（5-13）趋近于
，即仅取所有指标中最佳的代表方案整体情况。
注意到的闵式范数以p 变量为非减单调函数，即
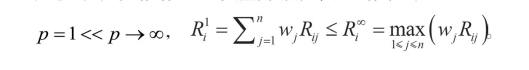
将非线性的闵式范数转化为操作简单的线性函数
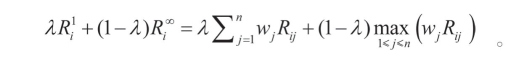
容易看出当λ =1 时，
当λ=0 时，
。
然而，怎样选择出一个合适的 p 值才该方法中最为困难的环节。针对p 值选择难题，学者Opricovic 提出了多指标妥协评价方法VIKOR[132，133]，该方法的原理是依据参数 p 在 Lp-metric中的单调性将 p 值的选择难题转换为通过一个取值范围是[0，1]的权重系数v 来寻求 L p=1，i和Lp=∞，i间的线性补偿或者说平衡，权重v 也随着成为最大整体效用策略的权重，转换后其表达式如下：
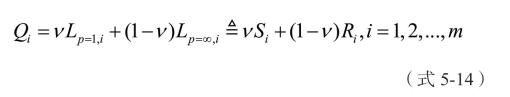
根据上述转化可知，求取 Qi 的关键显然是如何确定参数 ν 。因为ν 取值一旦确定，则妥协解可基于
求取，妥协排序也可以根据 Qi 降序排列来获取。
基于前文分析可知，医师绩效评价的指标间补偿体现在指标最大值和指标加权平均值在综合评价中所占比重，而该比重不同取值对应着不同的补偿策略，并进一步影响着医师绩效评价结果。确立医师绩效评价指标加权平均值和指标最大值，具体计算如下：
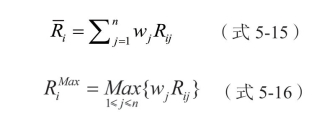
上式中wj为每项指标的权重，各指标总权重为1，即
。同时易知
，于是可形成
，当取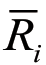
时表示完全补偿，当
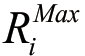表示完全不补偿，而数值在二者之间则反映在两种极端情形下的部分补偿规则。通常只能感官地给出允许指标间补偿程度，由于决策者的不同态度倾向，用语言术语描述（例如“补偿一点点”，“少许补偿”，“补偿一些”）对决策者而言应当是方便可行的。本文将在下一节展开详细论述。
同理，可得指标惩罚值的计算公式如下：
