辅导员职业韧性对工作适应的直接影响
回归分析和相关分析这两种统计分析,都是度量两个及以上变量之间的关系。因此,确定变量之间是否存在着关系,是二者的共同起点。其研究目的的差异在于,相关分析度量的是变量之间关系的密切程度。回归分析则是确定变量间可能存在的数量关系,并找出一种能表达变量依存关系的合适的数学模型。因此,回归分析和相关分析是相辅相成的,当相关分析显示出变量之间具有紧密的作用关系时,就可以进一步通过回归分析获取这种关系作用的回归模型以及推算值,进而知道自变量(本书指辅导员的职业韧性)对因变量(本书指辅导员的工作适应三维指标)的解释力,从而对变量进行有效控制。
对人的研究领域中,更多的情况是,两个变量的关系可能只是呈现一种直线趋势,而非完全的直线关系。犹如下面这幅散点图所表示的,X与Y的关系不是直线,但这些散点的分布有明显的直线趋势。X与Y的对应关系可以使用一条直线表示,这条直线的数学形式就是:Y=a+bX,这就是回归方程,代表X与Y的线性关系。其中X是自变量,亦称预测变量;Y是因变量;a是个常数,表示该直线在Y轴上的截距,b也是个常数,表示该直线的斜率,叫作Y对X的回归系数。本研究的目的,旨在描述和解释辅导员的职业韧性对职业承诺、工作倦怠和组织公民行为的影响作用。这就需要使用回归分析,通过找出回归方程,来简洁说明一组自变量(职业韧性的8个因子)与因变量(3个工作适应力因子)之间的关系。因此,具体的回归分析如下:
(一)职业韧性对职业承诺的解释力分析
将职业韧性的8个因子作为自变量,职业承诺作为因变量,建立回归方程,有1107个有效样本纳入此次回归分析。
从回归模型摘要表(表5-9)中得知,职业韧性的8个因子与职业承诺的多元相关系数是0.487(R),决定系数是0.237(R2),表示8个预测变量一共可以解释“职业承诺”23.7%的变异量。F值=42.633,显著性检验的p值为0.000,小于0.001的显著水平。表示回归模型整体解释变异量达到显著水平,回归方程式中至少有一个回归系数不等于0,或者说至少有一个预测变量会达到显著水平,而至于是哪些回归系数达到了显著,还要从回归系数摘要表中相关统计量来判断。
表5-9 辅导员职业承诺对职业韧性的回归模型摘要表

从回归系数摘要表(表5-10)中得知,8个预测变量的TOL在0.610—0.748之间,大于检测标准0.10,VIF在1.337—1.638之间,小于检测标准10,说明8个自变量间不存在多元共线性问题。
职业承诺对8个预测变量的非标准化回归系数在-0.026至0.182之间(B),非标准化回归系数通常用于以回归方程式来估计样本的预测值,但因为包含常数项,因此无法比较预测变量之间谁对因变量的重要性更大,而标准化回归系数因为已经去除单位的影响,因此可以作为自变量间解释力的比较。
表5-10 辅导员职业承诺对职业韧性的回归系数摘要表
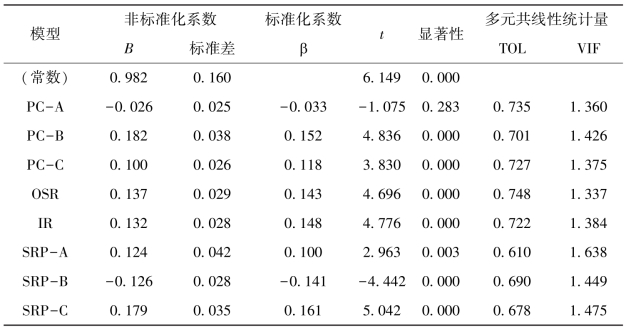
注:多元共线性,即数学上的线性相依,是指在回归模型中预测变量本身之间有很高的相关。如果共线性高,回归所估计的参数值的变异量就会变得很大,造成回归分析的情境困扰,导致被选入回归模型的预测变量的回归系数无法解释的矛盾现象。常用的共线性评鉴指标有容忍度(TOL)和方差膨胀因子(VIF),当TOL>0.10,VIF<10时,表明预测变量之间不存在多元共线性问题。
在表5-10中,8个预测变量的标准化回归系数在-0.033至0.161之间,从绝对值大小来判断预测变量对因变量的影响力大小,排序关系是:
SRP-C(16.1%)>PC-B(15.2%)>IR(14.8%)>OSR(14.3%)>SRP-B(14.1%)>PC-C(11.8%)>SRP-A(10.0%)>PC-A(3.3%)。
由此得到的标准化回归方程式是:
职业承诺=0.161×SRP-C+0.152×PC-B+0.148×IR+0.143×OSR-0.141×SRP-B+0.118×PC-C+0.100×SRP-A-0.033×PC-A。
由此可见,除了个体情绪特征之外,其余7个职业韧性因子的回归系数显著性检验t值达到了显著性水平,其绝对值在2.963至5.042之间。只有个体情绪特征PC-A因子的回归系数不显著,说明个体情绪特征对职业承诺的负向影响作用不明显。在削弱辅导员职业承诺的自变量中,行为自我调节过程SRP-B的预测力具有明显作用。
职业韧性因子对职业承诺的预测力中,排在前三位的韧性因子是:认知自我调节过程SRP-C,对职业承诺的解释量占到了16.1%;个体行为特征PC-B,对职业承诺的解释量占到了15.2%;压力应对的初始反应IR,对职业承诺的解释量占到了14.8%。其中,职业韧性的自我调节过程对职业承诺的解释量占到了40.2%,说明过程性保护因素对辅导员的职业承诺具有较高的预测效力。提示,可以通过干预辅导员的压力自我调节资源,来提升其在职业逆境中的职业承诺。
(二)职业韧性对组织公民行为的解释力分析
将职业韧性的8个因子作为自变量,组织公民行为作为因变量,建立回归方程,有1107个有效样本纳入此次回归分析。详细统计结果如下:
从回归模型摘要表(表5-11)中得知,职业韧性的8个因子与组织公民行为的多元相关系数是0.576(R),决定系数是0.332(R2),表示8个预测变量一共可以解释“组织公民行为”33.2%的变异量。F值=68.231,是对这个变异量显著性的检验结果,p值为0.000,达到了p<0.001的显著水平,说明该回归模型的整体解释变异量是显著的,意味着在这个回归方程式中,至少有一个预测变量达到了显著水平,而此回归系数到底是谁,还要从回归系数摘要表中相关统计量来判断。
表5-11 辅导员组织公民行为对职业韧性的回归模型摘要表

从回归系数摘要表(表5-12)中得知,8个预测变量的TOL在0.610-0.748之间,大于检测标准0.10,VIF在1.337-1.638之间,小于检测标准10,说明8个自变量间不存在多元共线性问题。
表5-12 辅导员组织公民行为对职业韧性的回归系数摘要表
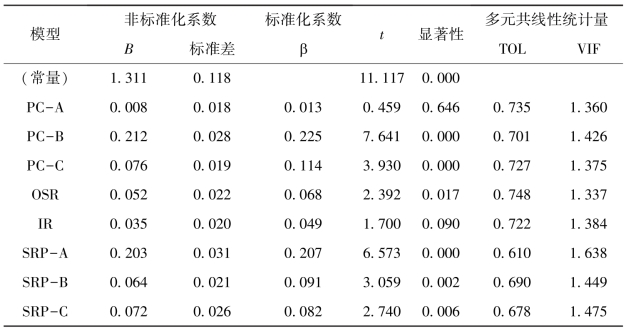
组织公民行为对8个预测变量的非标准化回归系数在0.008至0.212之间(B),标准化回归系数在0.013至0.225之间,从绝对值大小来判断预测变量对因变量的影响力大小,排序关系是:
PC-B(22.5%)>SRP-A(20.7%)>PC-C(11.4%)>SRP-B(9.1%)>SRP-C(8.2%)>OSR(6.8%)>IR(4.9%)>PC-A(1.3%)。
由此得到的标准化回归方程式是:
组织公民行为=0.225×PC-B+0.207×SRP-A+0.114×PC-C
+0.091×SRP-B+0.082×SRP-C+0.068×OSR+0.049×IR+0.013×PC-A。
职业韧性的因子中,有6个因子的回归系数的显著性检验t值达到了显著性水平,在2.392至7.641之间,均为正数,说明它们都对组织公民行为有正向的影响,回归系数不显著的预测变量是个体情绪特征PC-A因子、压力应对的初始反应IR因子,显著性检验t值分别为0.459与1.700,说明这两个职业韧性的因子对组织公民行为的预测作用不明显。
职业韧性因子对组织公民行为的预测力中,排在前三位的韧性因子是:个体行为特征PC-B,对组织公民行为的解释量占到了22.5%;情绪自我调节过程SRP-A,对组织公民行为的解释量占到了20.7%;个体认知特征PC-C,对组织公民行为的解释量占到了11.4%。其中,职业韧性的自我调节过程对组织公民行为的解释量占到了38%,说明过程性保护因素对辅导员的组织公民行为具有较高的预测效力。提示,可以通过干预辅导员的压力自我调节资源,来提升其在职业逆境中的组织公民行为。
(三)职业韧性对工作倦怠的解释力分析
以辅导员职业韧性的8个因子为自变量,辅导员工作倦怠为因变量建立回归方程,有1107个有效样本纳入此次回归分析。详细统计结果如下:
从回归模型摘要表(表5-13)中得知,职业韧性的8个因子与工作倦怠的多元相关系数是0.669(R),决定系数是0.447(R2),表示8个预测变量一共可以解释“工作倦怠”44.7%的变异量。F值是111.117,是对这个变异量显著性的检验结果,p值为0.000,达到了p<0.001的显著水平,说明该回归模型的整体解释变异量是显著的,意味着在这个回归方程式中,至少有一个预测变量达到了显著水平,而此回归系数到底是谁,还要从回归系数摘要表中相关统计量来判断。
表5-13 辅导员工作倦怠对职业韧性的回归模型摘要表

从回归系数摘要表(表5-14)中得知,8个预测变量的TOL在0.610-0.748之间,大于检测标准0.10,VIF在1.337—1.638之间,小于检测标准10,说明8个自变量间不存在多元共线性问题。
表5-14 辅导员工作倦怠对职业韧性的回归系数摘要表
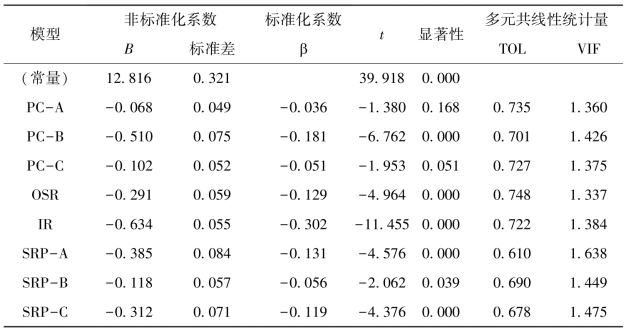
工作倦怠对8个预测变量的非标准化回归系数在-0.068至-0.102之间(B),标准化回归系数在-0.036至-0.302之间,从绝对值大小来判断预测变量对因变量的影响力大小,排序关系是:
IR(30.2%)>SRP-A(13.1%)>OSR(12.9%)>PC-B(18.1%)>SRP-C(11.9%)>SRP-B(5.6%)>PC-C(5.1%)>PC-A(3.6%)
由此得到的标准化回归方程式是:
工作倦怠=0.302×IR-0.131×SRP-A-0.129×OSR-0.181×PC-B-0.119×SRP-C-0.056×SRP-B-0.051×PC-C-0.036×PC-A。
职业韧性因子中,有6个因子的回归系数的显著性检验t值达到了显著性水平,在-11.455至-2.062之间,均为负数,说明职业韧性的这6个因子对工作倦怠都有削弱作用。回归系数不显著的预测变量是个体情绪特征因子PC-A和个体认知特征因子PC-C,显著性检验t值分别为-1.380与-1.953,说明这两个韧性因子对辅导员工作倦怠的保健作用不明显。
职业韧性因子对辅导员工作倦怠的预测力中,排在前三位的韧性因子是:对压力应对的初始反应IR,该韧性因子对辅导员工作倦怠的解释量占到了30.2%;情绪自我调节过程SRP-A,对辅导员工作倦怠的解释量占到了13.1%;社会支持资源OSR,对辅导员工作倦怠的解释量占到了12.9%。其中,职业韧性的自我调节过程对辅导员工作倦怠的解释量占到了25.6%,说明过程性保护因素对辅导员工作倦怠具有较高的预测效力。提示,可以通过干预辅导员的压力自我调节资源,来改善其工作倦怠。
