统计验证:有调节的中介模型
(一)共同方法偏差检验
所谓共同方法偏差,指因为同样的数据来源、同样的测量环境、同样的项目语境以及项目本身特征,或者是同样的评分者,这些因素造成了预测变量与校标变量之间出现了一种人为性的共变关系。可见,共同方法偏差属于一种系统误差,这种现象广泛存在于社会行为科学研究中,尤其是在问卷法的研究中。共同方法偏差这种人为的共变关系,对研究结果有严重的混淆影响,而且对研究结论有潜在的误导。
控制共同方法偏差的办法有程序控制与统计控制两种。程序控制是指研究者在研究设计与测量过程中采取的控制措施。包括:①平衡测量项目的顺序效应以及改进量表项目;②将测量的时间、空间和方法等影响要素之间做分离性处理;③采用被试匿名法来降低其对测量目的的猜度动机;④从不同来源来测量研究的预测变量和结果变量等。控制共同方法偏差的首选办法是程序控制,这种设计直接针对的是共同方法偏差的来源。其次是统计控制,这是在数据分析时对共同方法偏差的控制办法。Harman单因素检验法是最常用的统计控制,Harman单因素检验法假设,在共同方法偏差比较突出时,对数据的因素分析结果就会出现以下两种情况——或者是单独析出了一个因子,或者是在诸多析出的因子中,某个因子解释了大部分变量的变异。
按照此假设,倘若因素分析的结果只有一个特征值大于1的因子(这就表示只有一个因子),且该因子对总体变异的解释量超过40%(这表示该因子对总体变异的解释量太高了),这时就有理由认为共同方法偏差比较严重,这时就要停止基于该结果所做的任何进一步的推论。
本研究中,首先通过程序控制来减少共同方法偏差,包括改进量表项目、调整测量项目顺序、在不同时间地点取样、实测者不同以及匿名调查等等。其次采用Harman单因素检验法进行共同方法偏差的检验,结果表明,特征值大于1的因子共析出了16个,且第一个因子解释的变异量为16.04%,小于40%的临界值,说明共同方法偏差不明显。
(二)各变量的均值、标准差及相关关系
相关分析是度量两个及以上变量之间关系密切程度的统计方法。相关系数值介于-1至+1之间,绝对值越大,表明变量间的关联性越强。在推论统计中,不能单从相关系数绝对值大小来判断两个变量间的相关是否达到显著,必须结合显著性检验的概率值P来判断,只有当P<0.05时,才表明相关系数的显著性不是偶然造成的,才具有统计学意义。
表5-16 各变量的均值、标准差和相关系数
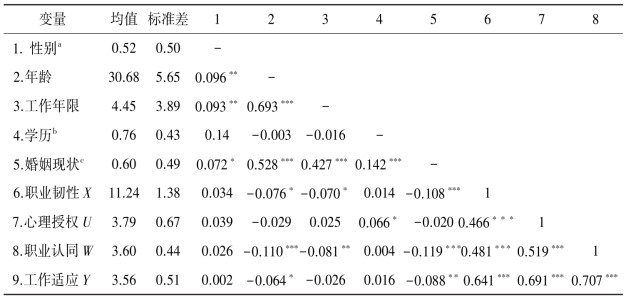
注:N=1107。性别、教育和婚姻均为虚拟变量,a女生=0,男生=1,均值表示男生所占比例;b专科本科学历=0,研究生学历=1,均值表示研究生所占比例;c单身=0,已婚=1,均值表示已婚者所占比例。*p<0.05,**p<0.01,***p<0.001(双尾检验)。
从表5-16可见,辅导员的职业韧性、职业认同、心理授权与工作适应之间的两两相关均达到显著性水平,而且都是正向相关,说明四者之间具有方向一致的公变关系,辅导员在一个心理特征上的水平越高,在另一个心理特征上的水平也会随之升高。在辅导员的五种人口学变量中,性别与四个职业心理变量的相关均不显著,但年龄、婚姻状态与职业韧性、职业认同和工作适应的相关显著,且均为负相关。说明年龄越大的高校辅导员和已婚的高校辅导员,在职业韧性、职业认同和工作适应上的水平反而越低。此外,从相关表中显示的是,辅导员的受教育程度越高,其心理授权的水平越高。
(三)有调节的中介模型之统计检验
为了避免多重共线性的出现,首先对所有预测变量做标准化处理(即均值为零)。然后将自变量、中介变量和调节变量的Z分数相乘,产生交互作用项UX和UW的分数。根据温忠麟、叶宝娟(2014)和Hayes(2013)的观点,在检验有调节的中介模型时,需要估计3个回归方程的参数。本研究中构建的3个方程如下:
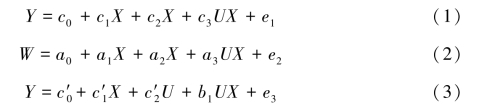
方程1估计调节变量(心理授权)对自变量(职业韧性)与因变量(工作适应力)之间关系的调节效应;方程2估计调节变量(心理授权)对自变量(职业韧性)与中介变量(职业认同)之间关系的调节效应;方程3估计调节变量(心理授权)对中介变量(职业认同)与因变量(工作适应力)之间关系的调节效应,以及自变量(职业韧性)对因变量(工作适应力)残余效应的调节效应。
数据分析时,在每个方程中对所有预测变量进行了标准化处理,并对年龄、受教育程度、婚姻和工作年限等变量进行控制,虽然性别与职业韧性、心理授权、职业认同和工作适应的相关均不显著,相关系数在0.002—0.039之间(p>0.05),但考虑到以往研究结果的争议性,为了保守起见,本书对性别变量依然进行了控制。所有预测变量方差膨胀因子(VIF)数值均不高于1.37,低于评判指标值10,因此不存在多重共线性问题。
本研究分七步来检验有调节的中介模型:即职业韧性(X)通过职业认同(W)影响工作适应力(Y)的中介过程,是否受到了心理授权(U)的调节。
第1步,对预测变量和校标变量做标准化处理。然后将自变量、中介变量和调节变量的Z分数相乘,产生交互作用项UX和UW的分数。在多元回归分析中,对性别、年龄、工作年限、受教育程度和婚姻状况等人口学变量进行控制。统计时分别将性别、受教育程度和婚姻等三个类别变量,转化为虚拟变量[2]。
第2步,对回归方程(1)的参数进行估计(见表5-17)。结果显示,方程(1)整体上显著,F=196.935(P<0.001)。其中,多元相关系数(R)为0.786,决定系数(R2)为0.618,调整后的R2为0.615,表示8个预测变量总共可解释校标变量(工作适应力,Y)61.5%的变异量。上述8个预测变量的方差膨胀系数值(VIF)在1.009—2.205之间,低于评判指标值10,表示进入回归方程式的预测变量之间不存在多重共线性[3]问题。
表5-17 职业韧性、心理授权预测工作适应力的回归分析
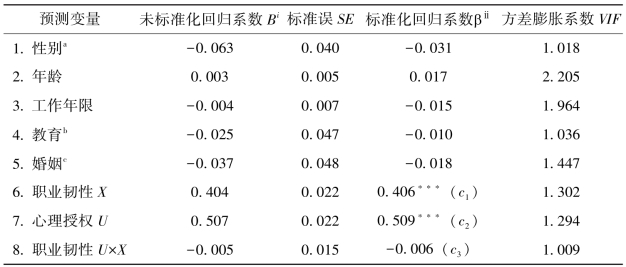
注:ⅰ未标准化的回归系数包含常数项,无法比较预测变量的相对重要性。ⅱ标准化系数已去除了单位的影响,因此可以作为预测变量间解释力的比较。a女生=0,男生=1,均值表示男生所占比例;b专科本科学历=0,研究生学历=1,均值表示研究生所占比例;c单身=0,已婚=1,均值表示已婚者所占比例。*p<0.05,**p<0.01,***p<0.001(双尾检验)。
如表5-17所示,辅导员的职业韧性(X)对工作适应力(Y)的正向预测效应显著(c1=0.406,t=17.984,p<0.001),辅导员的心理授权水平(U)对工作适应力(Y)的正向预测效应显著(c2=0.509,t=22.612,p<0.001)。而职业韧性与心理授权的交互项(UX),对工作适应力(Y)的负向预测作用是不显著的(c3=-0.006,t=-0.300,p=0.764)。c3不显著,说明在不考虑中介效应的时候,职业韧性(X)对工作适应力(Y)的直接效应没有受到心理授权(U)的调节。
第3步,对回归方程(2)的参数进行估计(见表5-18)。结果显示,方程(2)整体上显著,F=68.266(P<0.001)。其中,多元相关系数(R)为0.599,决定系数(R2)为0.359,调整后的R2为0.354,表示8个预测变量总共可解释校标变量(职业认同,W)35.4%的变异量。上述8个预测变量的方差膨胀系数值在1.009—2.205之间,低于评判指标值10,表示进入回归方程式的预测变量之间不存在多重共线性问题。
表5-18 职业韧性、心理授权预测职业认同的回归分析
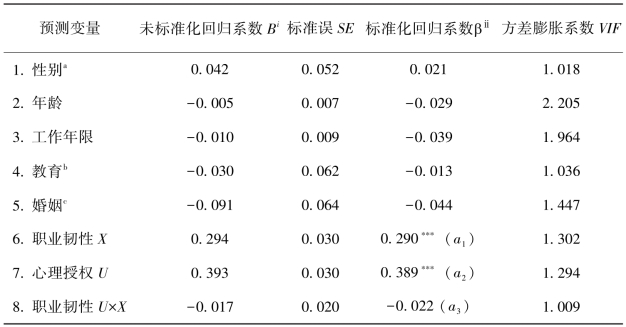
注:同表5-17。
如表5-18所示,辅导员的职业韧性(X)对职业认同(Y)的正向预测效应显著(a1=0.290,t=9.917,p<0.001),辅导员的心理授权水平(U)对职业认同(Y)的正向预测效应显著(a2=0.389,t=13.321,p<0.001)。而职业韧性与心理授权的交互项(UX),对职业认同(Y)的负向预测作用是不显著的(a3=-0.022,t=-0.861,p=0.389)。
第4步,对回归方程(3)的参数进行估计(见表5-19)。结果显示,方程(3)整体上显著,F=265.521(P<0.001)。其中,多元相关系数(R)为0.843,决定系数(R2)为0.711,调整后的R2为0.708,表示9个预测变量总共可解释校标变量(工作适应力,Y)70.8%的变异量。上述9个预测变量的方差膨胀系数值在1.021—2.207之间,低于评判指标值10,表示进入回归方程式的预测变量之间不存在多重共线性问题。
表5-19 职业韧性、心理授权、职业认同预测工作适应力的回归分析
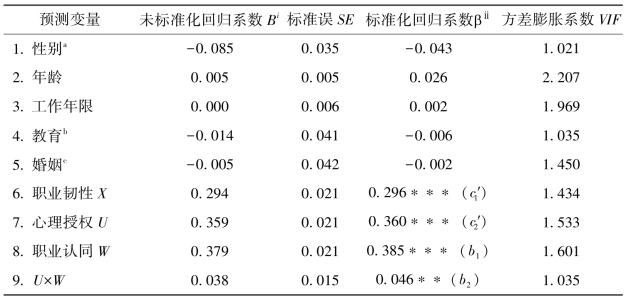
注:同表5-17。
如表5-19所示,辅导员的职业韧性(X)对工作适应力(Y)的正向预测效应显著(c1′=0.296,t=14.319,p<0.001),辅导员的心理授权水平(U)对工作适应力(Y)的正向预测效应显著(c2′=0.360,t=16.880,p<0.001),职业认同(W)对工作适应力(Y)的正向预测效应显著(b1=0.385,t=14.319,p<0.001),职业认同与心理授权的交互项(UW),对工作适应力(Y)的正向预测作用是显著的(b2=0.046,t=0.966,p<0.01)。
第5步,根据有调节的中介模型应具备的两个条件,来检验中介效应是否随调节变量的变化而变化。这两个条件是:
条件一:在方程(1)中,预测变量X对校标变量Y的总效应(c1)显著;
条件二:在方程(2)和(3)中,预测变量X对中介变量W的效应(a1)显著,中介变量W与调节变量U对校标变量Y的交互效应(b2)显著,和/或预测变量X与调节变量U对中介变量W的交互效应(a3)显著,中介变量W对校标变量Y的总效应(b1)显著。
简单地说,如果a1≠0(显著表示为不等于)且b2≠0,或者是a3≠0且b1≠0,或者是a3≠0且b2≠0,至少有一组成立,就说明中介效应受到了调节,即有调节的中介模型成立。本研究中,a1显著(a1=0.290,t=9.917,p<0.001)且b2显著(b2=0.046,t=0.966,p<0.01),说明有调节的中介模型成立,即辅导员的职业韧性通过职业认同的中介过程,影响着辅导员的工作适应力,而且该中介过程还受到了辅导员心理授权水平的调节。在该模型中,只有中介效应的后半路径受到了心理授权的调节,模型见图5-6。在该模型中,中介效应就等于中介路径上两个路径系数的成绩{a1(b1+b2U)}。
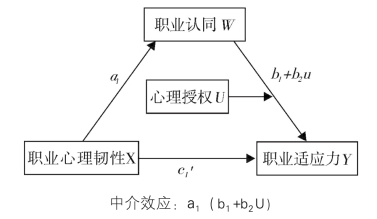
图5-6 职业韧性对辅导员工作适应力的有调节的中介模型(中介效应)
第6步,依据以上获得的参数,绘制的有调节中介模型如图5-7。通过这些估计的参数,能计算出中介效应,即辅导员的职业韧性对工作适应力有调节的中介效应是0.290×(0.385+0.046)。当U取均值时,中介效应为0.117(即0.290×0.385);当U取均值以上一个标准差时,中介效应为0.125[即0.290×(0.385+0.046)];当U取均值以下一个标准差时,中介效应为0.098[即0.290×(0.385-0.046)]。而职业韧性对工作适应力的总效应为0.641(即X对Y的直线回归系数),如此,当U取值分别为-1、0、1时,中介效应分别占了总效应的15.3%、18.3%、19.5%。
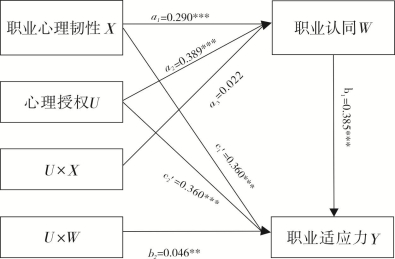
图5-7 职业韧性对辅导员工作适应的有调节的中介模型(路径系数)
第7步,为了更清楚的解释职业韧性与心理授权的相互效应实质,进行简单斜率检验,即将心理授权按正负一个标准差分出高低组,考察在不同心理授权水平上,职业韧性对职业认同的影响,并绘制简单效应分析图5-8。结果表明,对于低心理授权的辅导员群体来说,职业韧性对职业认同的促进作用较强(B=0.44,SE=0.03,t=14.59,p<0.001);而对于高心理授权的辅导员群体,这一关系明显较弱(B=0.28,SE=0.06,t=4.75,p<0.001;B由0.44减弱为0.28)。
根据“保护因子—保护因子模型”,倘若两种保护性因子同时对辅导员的职业认同产生影响时,这两种保护因素可能会发生交互作用,而且这种交互作用的模式并不总是一致的,可以表现为两种情况——相互促进和相互抑制。前者称之为“保护因子—保护因子模型”的促进假说,该假说认为,自变量(X)对调节变量(U)高分组个体的保护作用更强;后者称之为“保护因子—保护因子模型”的排除假说,该假说认为,自变量(X)对调节变量(U)低分组个体的保护作用更强。本研究中,职业韧性与心理授权均能促进个体的职业认同,两者都是辅导员职业认同的保护性因素。在辅导员职业认同的交互效应模式中,职业韧性与心理授权这两种保护因子对职业认同的影响具有排除假说的功能,而不是促进假说的作用。在这种对抗型交互作用模型中,一种保护因子(心理授权)会降低中介效应对结果变量(工作适应力)的影响。
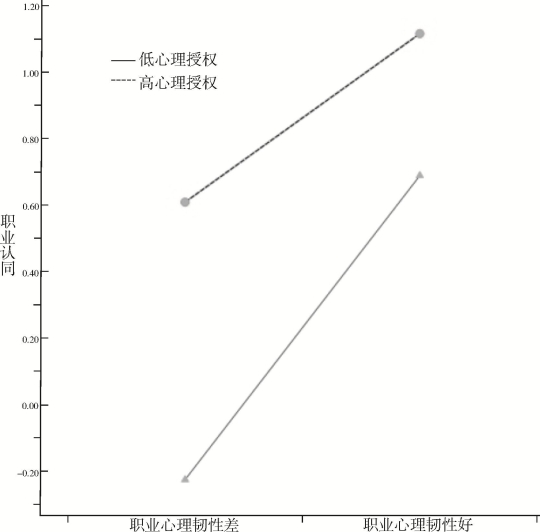
图5-8 辅导员心理授权水平对职业韧性与职业认同的调节作用
换言之,当辅导员对组织授权的主观体验(即心理授权)较低时,这时通过提高辅导员的职业韧性,可以更有效地改善其工作适应力。也就是说,对于低心理授权的辅导员而言,他们的职业韧性水平,对预测其工作适应力的效应更大。反之,当辅导员对组织授权的主观体验较高时,他们的职业韧性水平对工作适应力的预测效应会变小。此时,若想通过提高职业认同水平来进一步改善工作适应结果,这种干预策略的有效性会大打折扣,远不及在低心理韧性时的收效。由此可见,在高心理授权的辅导员中,职业韧性通过职业认同来间接影响工作适应的保护作用可能得不到显示,作为结果变量的工作适应力出现了“地板效应”。而在低心理授权的辅导员中,这种地板效应消失了,职业韧性通过职业认同对工作适应的中介效应才能有效发挥其保护作用。
