克服每一种思维障碍
如何使自己具有创新思维呢?这需要不断地训练这种转换能力。有几种办法有助于提高这个能力。其中之一就是针对思维障碍进行排除。因为任何观念的创新、创新设想的提出,不论大小、难易,都是相对一种或多种思维障碍而言的,谁能突破障碍,谁就能取得创新成果。人的思维障碍是通过以往的教育、社会习俗及常规解题习惯长期形成的,有一定的稳定性和危害性。克服思维障碍的关键是认识其有哪些具体表现,并有针对性地加以克服。针对上述思维障碍的十大表现,我们可以相应地采取如下方式进行思维:
(1)破除思维定势;
(2)保持怀疑态度——不迷信书本知识和权威;
(3)打破已有的规则、不安于现状,敢于想象;
(4)向唯一性发起挑战——多角度思考;
(5)变直线思维为变通思维;
(6)变抽象思维为具体化思维;
(7)排除问题情境的干扰;
(8)变简单思维为复杂思维;
(9)变夸大问题为简化问题;
(10)摆脱解题条件的限制。
例如,运用第(10)条的方式,摆脱解题条件的限制来解决问题:如图3-2所示,纸上有9个点,要把这9个点用直线全部串联起来,最少用连续的(不许跳跃)几条折线能办到?对这一问题,一般人的答案是5条折线(图3-3)。这说明大多数人附加了限制条件,就是所划的折线线段不能离开这9个点组成的方形点阵范围。

图3-2 九点问题
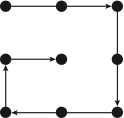
图3-3 用5条折线
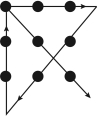
图3-4 用4条折线
事实上问题并没有这样限制我们,如果取消这个限制条件的限制,我们可以设想,用4条折线也可以串起9个点(图3-4)。有人认为,问题条件也没有说明黑点多大,如果黑点足够大,可以只用连续的3条直线,每一条线不一定经过各点的中心处(图3-5)。还有个设想是,问题条件也没有限制不让折叠纸张,将画有黑点的纸适当地折起来,使9个点合在一条线上,用笔画一条线,也可以穿过所有的黑点(图3-6)。另一解法是把纸贴在地球仪或其他球状物体上,用一条线根本不用折一下也可以将9个点连起来(图3-7)。但最好的回答思路是问题条件没有说用什么样的笔。用一个与9个点组成图形一样宽的油墨刷,只轻轻一刷将9个点全部盖住(图3-8),这也是一种“联”法。显然这是最富创造力的,因为问题没有限制解题人不能用粗笔,也没说这9个点距离很远。
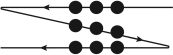
图3-5 用3条折线
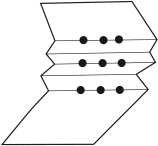
图3-6 用1条折线
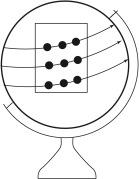
图3-7 用1条折线
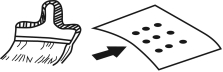
图3-8 最富创造的方式
当然克服思维障碍本身并不容易,这本身也会存在思维上的障碍,为此,人们设计了一些方法,来促使人们更容易地克服思维障碍,所以,创新方法中很多都是针对克服一个或几个思维障碍而设计的,比如,小人法、STC算子法、强制联想法、盒内思考法、六顶思考帽法等等。
