2.2 数学模型的建立
轴系响应的研究是转子动力学的主要内容之一，计算方法主要是模态叠加法，直接的时域积分法，和传递矩阵法三类。传递矩阵法和时域积分法都能运用于非线性。对于转子这样的传统的链式系统，传递矩阵法具有优越性。所以我们建模也采用传递矩阵法。
2.2.1 轴系的建模
为了便于计算分析，首先对实际的轴系进行集总化处理，把无穷多个自由度的系统离散成为具有若干集总质量的多自由度系统。即沿轴线把轴系的质量及转动惯量等集总到若干个结点（或称圆盘）上，这些结点一般选在叶轮，支承中心，轴截面突变处，以及轴的端面处，关于轴系的集总化处理，在转子动力学中已经有非常详细的介绍，此处不再具体给出。
（1）转子本身的建模。大型混流式水轮机的主轴，由上结轴，发电机轴，电机轴，水轮机轴，发电机转子和水轮机转轴组成。根据转子动力学，轴比较粗短，所以转动惯量比较大，应考虑回转效应，摆度惯性和剪切效应。发电机转子和水轮机转子都是非常重要的部件，建模时对两者处理不一样，结果也有很大的差异。发电机转子的弯曲刚度仅考虑中心体即可，简单地看成一个刚性薄盘，转轮的形状比较复杂，计算也相对复杂得多，这里我们只是把它考虑成一个厚圆筒。另为水轮机在带负荷运转时，转轮的叶片间充满了水，所以要考虑转轮的附加质量，根据有关资料，我们考虑水的附加质量是相应结点的质量的20%来进行计算。
（2）支承边界条件的考虑。水轮机组的各个导轴承，多是采用多瓦块构成的可倾瓦式滑动轴承，其油膜特性，在力学上采用8个动力特性系数来表示，这8个系数组成了刚度矩阵和阻尼矩阵，即
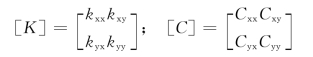
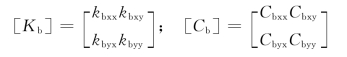
相应的轴承座及基础可简化成质量弹簧系统来表示，其刚度阻尼矩阵分别为：如果考虑油膜力是线性的，那么以上的各个特性系数都是常数，考虑成非线性，那么这些系数都是时变的，则整个支承可以简化为如图3所示。
轴系中推力轴承，主要承受机组的重量和轴向水推力，并把它们传递给机架。推力轴承对轴系的轴向振动的影响并没有导轴承那么明显，但也不能忽略，常把它视为一个扭转弹簧，但系数很难能得到，而且实用性并不高，所以这里不再考虑。
发电机转子本身由于电磁作用，将受到不平衡的电磁拉力的影响。根据有关资料，可以把它考虑成一个具有负刚度的支承。
轴系上的装有一些不锈钢轴衬，以及止漏环密封套等一类附加件，其对轴系的影响也不能忽略。按比例集总其质量和转动惯量到结点上去，并适当放大外径求解轴段的抗弯刚度。到此，我们已经可以给出物理力学模型，每一个结点的力学微分方程为：
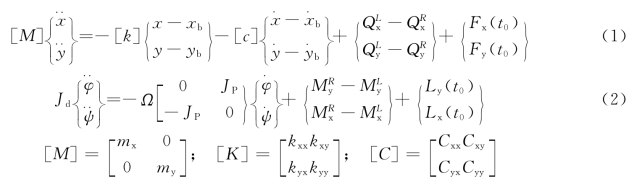
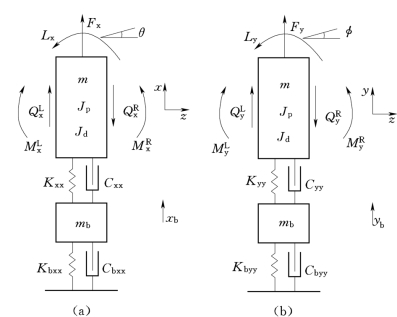
图3 支承的简化过程
（a）X轴方向；（b）Y轴方向
式中：Fx、Fy、Lx、Ly分别是作用在结点上的x和y方向的外加任意激励力和力矩；Ω为转子的转动角速度；
分别是结点左、右截面两坐标方向上的剪力；
分别是结点左右截面两坐标方向上的弯矩。同样地，支承的运动微分方程是：
2.2.2 Newmark-β方法
根据Newmark-β方法，取γ=1/2公式为：
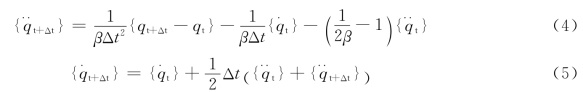
式中：
分别为t和t+Δt时刻的位移，速度与加速度，且都是广义的。可以根据上面的公式求得在t+Δt时刻的速度和加速度，而位移则由Riccati传递矩阵法求得。那样逐步递推，将能得到后面各个时刻各个结点的位移量，即各个结点两个方向的摆度。
2.2.3 部件的传递矩阵
将式（4）和式（5）代入式（1）和式（2）并引入状态向量f={Mx、Qx、My、Qy}T；e={x，f，y，ψ}T。根据转子动力学及相关资料，把结点i和它右边的轴段一起组成一个组合部件，其传递方程为：
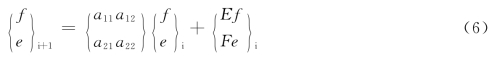
式中：a11、a12、a21、a22、Ff、Fe，在转子动力学与其他文献中已有叙述，此处不再给出。
2.2.4 响应的求解
引入Riccati变换式fi=Siei+Pi，把它代入式（6）中，可以得到Si和Pi的递推关系式：
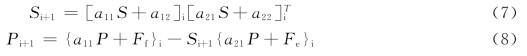
根据轴系的边界条件，在上接轴的上端面，f1=0e1=0。所以可以推出S1=0，P1=0；从而根据上面的公式可以逐步地推出每一个结点S和P，而在最后一个结点上，根据边界条件fN=0（N为结点数）所以eN=
在利用前后结点的递推关系式：
据此，可以知道各个结点在某一时刻的位移值，也就知道了各个时刻三导处的摆度值。
2.2.5 模型的修正
由于模型进行了简化，由上面的模型求解得到摆度值跟实验测得的数据有较大的差距，要对模型进行修正，通过添加附加力的办法来修正模型，先根据理论计算得到一组摆度值，再把实验测得某一时刻的摆度代入式（4）和式（5）求得实验数据的速度和加速度。分别把前面理论计算和实验测得的摆度值、速度值、加速度值代入式（1）得到：
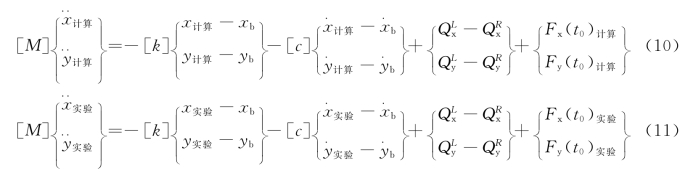
考虑剪切力两者是一样的，两者相减就可以得到Fx（t0）实验和Fy（t0）实验，把这两者当作所结点所受的外力代入模型。即在结点上附加了
大小的外力，此时模型得到了修正，重新进行计算就可以求得结点的摆度值。