3.2 小波分析除噪
在信号处理领域，用小波方法除噪已得到了越来越广泛的应用。小波去噪的方法有多种。常用的有小波分解与重构法去噪和非线性小波变换阀值法去噪。
3.2.1 小波分解与重构法
若f（k）为信号f（t）的离散采样数据，fk=C0，k。则信号f（t）的正交小波变换分解公式为：
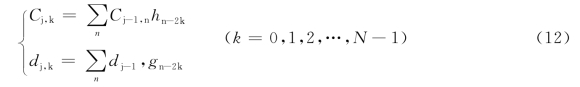
式中：Cj，k为尺度系数；dj，k为小波系数；h、g为一对正交镜像滤波器组；j为分解层数；N为离散采样点数。
小波重构过程是分解过程的逆运算，相应的重构公式为：
小波分解与重构法去噪具体步骤：根据需要，将含有噪声信号在某一尺度下分解到不同的频带内，然后再将噪声所处的频带置零（或直接提取有用信号所在的频带），进行小波重构，从而达到去噪的目的。
3.2.2 非线性小波变换阀值法
此方法利用信号和噪声在小波变换下的不同的特性，通过对小波分解系数进行处理来达到信号和噪声分离的目的。在水电机组故障诊断中，有用故障信号通常表现为低频信号，而噪声信号则通常表现为高频信号。可以先对含噪信号进行小波分解，如进行三层分解，如图1所示。
其中CAi为分解的平滑部分，CDi为分解的细节部分，i=1，2，3。则噪声部分通常包含在CD1、CD2和CD3中，用门限阀值对小波系数进行处理，重构信号即可达到去噪的目的。总结去噪过程，可以分成以下三个步骤：
（1）一维信号的小波分解，选择一个小波并确定一个小波分解的层次N，然后对信号小波分解。
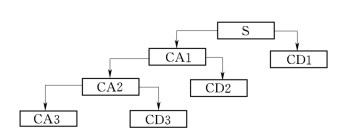
图1 原始信号小波分解过程示意图
（2）小波分解高频系数的阀值量化，对第1到第N层的每一层高频系数，选择一个阀值量化处理。
（3）一维小波的重构，根据小波分解的第N层的低频系数和经过量化处理后的第1层到第N层的高频系数，根据式（13）进行一维信号的小波重构。
由于白噪声在任何正交基上的变换仍然是白噪声，并且有着相同的幅度。相对来说，信号的小波系数值必然大于那些能量分散且幅值较小的噪声的小波系数值。选择一个合适的阀值，对小波系数进行阀值处理，就可以达到去除噪声而保留有用信号的目的。