1.1 双向流动计算基本方程
2026年01月15日
1.1 双向流动计算基本方程
在进行可逆转轮的反问题计算时,将转轮内的速度分解为周向平均和周期性脉动分量,用置于叶片中心面上的源汇涡来代替叶片对流场的作用,而叶片形状以满足流动边界条件迭代确定。
转轮内的速度可分解为平均流动和周期性脉动流动:
![]()
对平均流动![]() 引入流函数ψ和势函数φ:
引入流函数ψ和势函数φ:
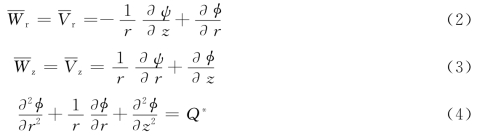
其中
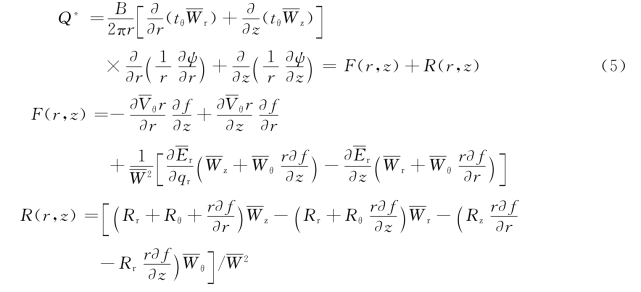 (https://www.daowen.com)
(https://www.daowen.com)
周期性脉动流动![]() 方程组为:
方程组为:
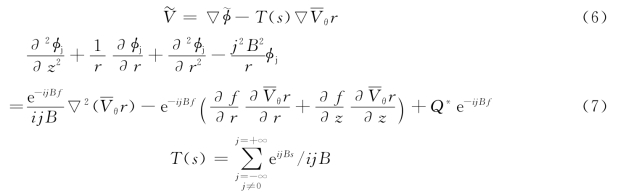
根据叶片表面相对流速与叶片表面相切及相对流速的展开式可得叶片方程为:
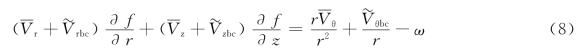
式中,![]() 为平均速度分量;
为平均速度分量;![]() 为相对流速的周期性分量。
为相对流速的周期性分量。
利用上述全三维反问题计算模型进行可逆转轮全三维设计时,求解反问题计算方程式(2)~式(7)可以得到反问题计算的流场;由于设计过程中求解速度的方程是由理想流体动力学方程直接推导出来的,因而也完全可以用于与设计方向相反流动的流场计算。
在进行正问题计算时,上述方程中叶片坐标f为反问题计算结果,视为已知参数,在计算过程中保持不变;沿设计方向相反的流动方向求解式(2)~式(5)得到平均流动,求解式(6)~式(7)得到周期脉动流动,两者叠加由式(1)即可得到转轮内的三维流动解。
