2.1 参数计算及效率值修正
对采集过来的参数值进行公式推导。本系统对水轮机流量Q采用伯努力方程的推导：
式中：K为水轮机蜗壳流量系数；Δh为蜗壳差压；通过差压传感器获得。
水轮机工作水头H可表示为：
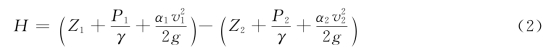
式中：Z1、Z2为电站上下游水位，从监控系统中获得；v1、v2为电站上下游平均流速；α1、α2为流速分布均匀系数，近似取α1=α2=1；P1、P2为蜗壳进口压力，通过压力传感器获得。
在效率试验过程中，由上下游水位波动和引水管道在通过不同流量时产生的水头损失不同，因而使各测次的水轮机工作水头略有波动。为比较同一水头下的效率特性，应将不同的开度下流量和功率的实测值按下式换算至同一平均水头下的值：
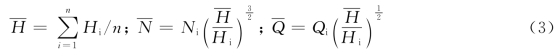
式中：Qi、Ni分别表示实测的流量、功率值；
分别表示换算至某一平均水头下的流量和功率；Hi为实测的水轮机工作水头；
为平均水头。则机组的效率ηu为：
对实测结果进行误差分析表明：效率测量的总误差fη由效率测量的系统误差和随机误差两部分组成。系统误差由流量系统误差fQs、水头系统误差fHs和功率系统误差fNs组成。本系统是通过蜗壳差压法测得的流量，经式（4）换算成效率，其中可能因为出现差压计及其附属管路中的气体未排尽或其他一些原因，使得测量数据的变化幅度超过允许的流量系统误差fQs范围，从而计算的流量
与真实值相差较大，从而导致计算得到的水轮机效率存在偏差。本系统使用理论流量和实测流量进行对比。以乌溪江湖南镇电站为例，根据2004年9月的厂方的效率试验报告，机组的流量系统误差fQs约为1.2%，根据不等式：
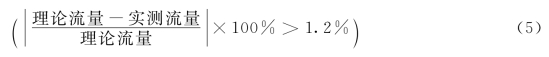
不等式成立则采用理论流量，反之采用实测流量。上述情况仅出现在流量测量过程中，所以对其他参数测量值不需要特别进行校验。
为了获得理论流量，需要在水轮发电机组运行综合特性曲线图上，通过二维插值算法获得机组的效率，然后通过公式
求得理论流量，图2为插值原理图。最后将经过比较后确定的效率值记录在数据库内。
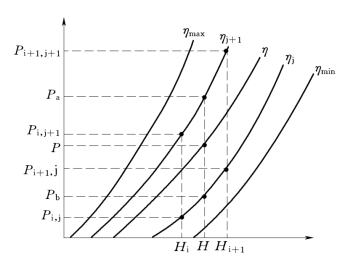
图2 效率插值原理图