2 明渠
河流和明渠的流量测量通常是借助率定曲线来进行计算的。它通过记录水位读数并将其转换成流量。率定曲线是通过对一组流量测量和水位数据进行分析,并进行周期性的检验,以确定它们之间的一种恒定不变的水位—流量关系曲线而得出的;许多现象会引起率定曲线的改变,因此,相同的记录水位可能会产生不同的流量。这是由于明渠下的可变水力学条件引起的,例如:回水效应、闸门或惟一的水位—流量关系曲线不存在。在这种条件下,应用超声波流量计是非常有意义的,而且能有效地进行水资源管理。事实上,只要不同的流量值可以与相关水力学特征的某一特定水位高程相对应,那么在流体中的超声波传播速度与流体本身总有一种惟一的对应关系。
利用超声波技术,通过明渠的流量可以采用超声波的单声路和多声路技术来确定。在单声路配置中为了能使渠底以上高程Z处的单一的线流速Vz达到精确的读数,必须特别注意应确定平均声路垂向流速的分布(图5)。另一方面,在多声路配置中平均线流速将被很好地描述。但在这种情况下应特别注意使用的积分方法,以用于根据当前声路的读数来确定流量。
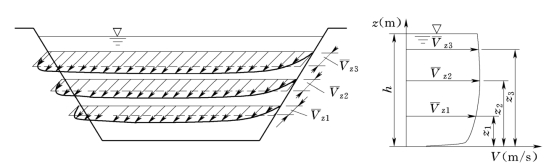
图5 由超声波流量计测量的流速和每一层的线垂向流速剖面
在单声路测量中,使用面流速方法,流量Q(m3/s)可通过Q=VmA计算出。其中Vm(m/s)代表面平均流速,A(m2)代表横截面积。为了获得穿过整个断面的平均流速Vm,可通过超声波流量计测得给定深度处的声路流速Vz,但这个流速并不等于平均流速,它必须通过一个水力校正系数K进行修正,因此根据关系式Vm=KVz可算出平均流速。通常,K系数反映水平和垂向流速剖面的影响。它主要取决于水位、断面形状和边界粗糙度。
该垂向流速可通过众所周知的对数定律来描述,见图6。计算公式为:
![]()
V(z)代表渠底以上高程Z处的流速,K代表一个常数,V代表切变流速,Z0代表一个积分常量,这个常量可以被看作是等于渠底到真实底部的一个假想的朝上的位移,它被用来解决积分问题。当边界表面很粗糙时,Z0仅与粗糙度高程有关,可根据关系式Z0=KS/30得出。对式(2)进行积分当Z0趋向于总水位高程时,流速可用Vm替代,可得到:

假定在高程h中可以忽略z0,在图6中对数公式中的K系数将表示两个不同的底部粗糙度系数。然而,在许多实际应用中,经常很难确定修正值Ks。基于这个原因,其他的以幂定律为基础的K形式得以发展。该垂向流速V(z),按照幂定律,可表示为:
![]()
式中,h代表实际的水位,Vs代表水表的线流速(最大值),1/m代表指数,见图7。在式(4)中,指数1/m如今已不再是一个常数,而是取决于影响管道形状的粗糙度和水力学半径。对式(4)进行积分,当Z趋向与总水位时,K系数可表示为:
![]()
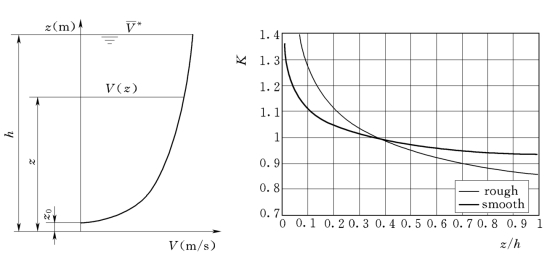
图6 对数定律:流速分布和在函数z/h中修正系数K的变化
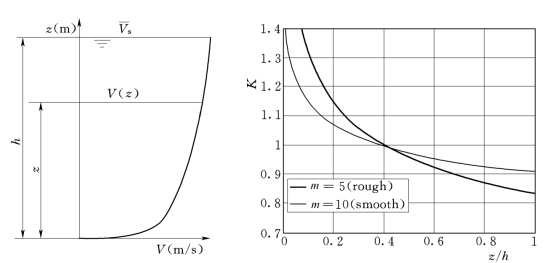
图7 幂定律:流速分布和在函数z/h中的修正系数K的变化
m值取决于粗糙度系数,可以利用Darcy-Weisbach的摩擦系数公式来表示,即:(https://www.daowen.com)

K系数在0.2~0.4之间变化,这是由悬浮颗粒的多少决定的(当低值时被测液体高度混浊),也可以用马宁公式来表示它们之间的关系,即:

g代表重力加速度,n代表马宁粗糙度系数,Rh代表水力学半径。在图7中,修正系数分别表示一个平滑和一个粗糙的表面。由于马宁公式形式简单、用途广、计算结果精确,因此已广泛应用于明渠流量计算,这使得其在现场应用很容易得以实现。
根据以前所述的明渠垂向流速剖面公式,我们可以预测,最大流速位于水表;然而现场和实验室测量后证明,该最大流速发生在水表之下,其强度取决于B/h的比值,B代表渠宽。这个发现表明,一维的流速分布定律并不能完全地描述明渠的流态分布,因此,为了减少不确定的流速剖面,同时为了即使在恶劣的流态条件下也能获得高精度的流量数据,就必须采用多声路配置。
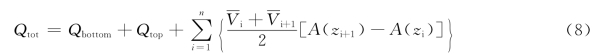
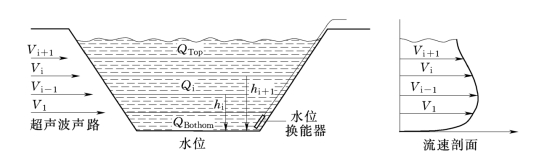
图8 多声路流量测量和流速剖面
在多声路测量中,使用平均断面法,即测量从水表到渠底之间的若干层的流速进行平均(图8),总流量Qtot将根据下列关系式得出:底部流量Qbottom是指最低声路之下的底部面积乘以底部流速得出的流量,其中底部流速是指通过渠底摩擦系数校正过的最低声路流速;顶部流量Qtop是指最高声路之上的顶部有效面积乘以顶部流速(Interpolated from the velocity profile)Vtop得出的流量,Vi代表第i声路的流速,A(zi)代表第i声路之下的横截面积。
为了分析单声路和多声路配置的性能和精度,在德国达木斯塔特工业大学的水力学院做了大量的实验室实验:渠道为39m长,2m宽,以电磁式流量计测得的流量作为参考,测量精度为0.5%。在这次测试中超声波流量计采用的是4声路配置。对于不同的水位,流量测量的范围从0.01到0.7m3/s变化。图9显示的是单声路和多声路布置下的误差分布图。在这里,P[Ei<E<Ei+1]代表可能性的相对误差E将位于[Ei,Ei+1]之间。
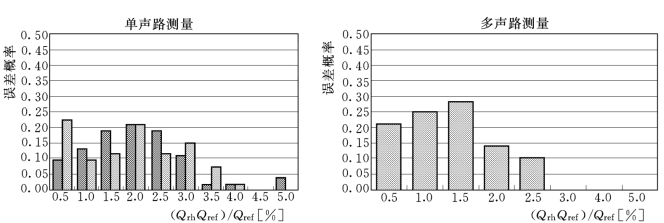
图9 单声路和多声路下的误差分布
为了证明其稳定性和可靠性,由意大利帕多瓦大学的水力学院和ENEL′s水力建筑研究中心联合进行了一次详细的测试分析。以一台流速计作为参考,分别在农用灌溉渠和水利明渠中采用不同的超声波声路配置进行了现场测试(图10),在农用灌溉渠中安装了一台单声路超声波流量计,在水利明渠的出口安装了一台交叉双断面多声路流量计。图11给我们显示的是所有的测量点和确认点。由图表我们可以看出,即使在现场条件下应用,超声波流量计一样能够实现和实验室一样的高精度结果。
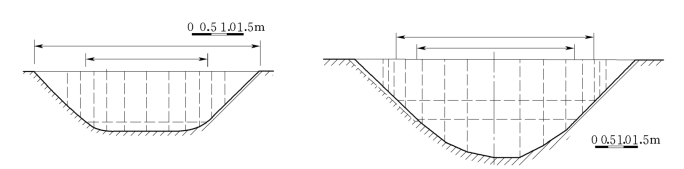
图10 测量断面的几何尺寸
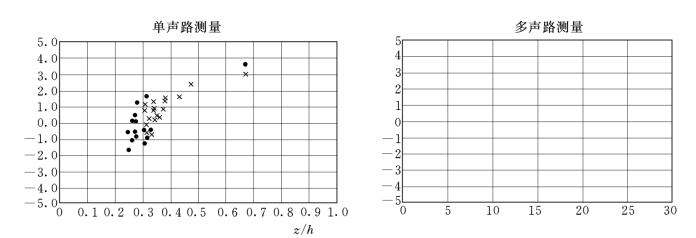
图11 现场应用:单声路和多声路配置下的测试结果
