2 自相关
定义1：设f（t）为实随机信号，周期为T，定义f（t）在τ时刻的自相关函数R（τ）为：
式中f（t）的傅立叶级数展开为：
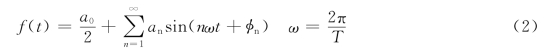
根据自相关函数R（τ）的定义可以推出：
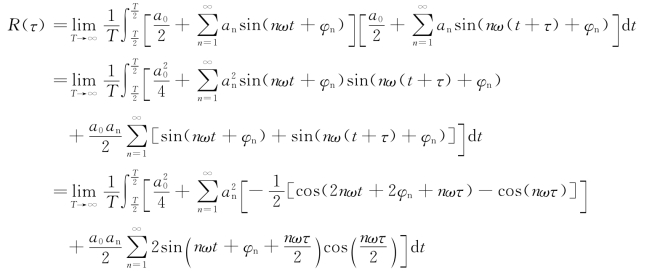
因为sin（t）为奇函数，它在对称区间上的积分为0，
=sin（nωT）=sin（2nπ）=sin（0），
=sin（-nωT）=sin（-2nπ）=sin（0），则可推出：
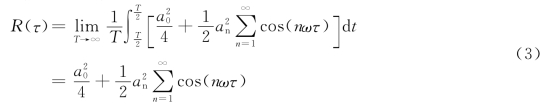
可以看出，R（τ）和f（t）具有相同的频率成分，且R（τ）的各频率成分的振幅是f（t）各频率成分振幅平方的一半。
离散序列{X（i）|i=1，2，…，N}（N为采样点数）的自相关函数表示为：
一般情况下水电机组故障信号S（t）包含两个部分：有用信号C（t）和白噪声信号N（t）。白噪声是由各种频率的谐波组成，幅值相近，分布均匀，没有突出的频率成分。故障信号S（t）可表示为：
故障信号S（t）经过采集后成为信号序列{Sk|k=1，2，…，N}，它的自相关序列：
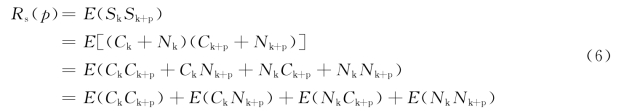
因为噪声与有用信号之间是互不相关的，则E（CkNk+p）=E（Ck+pNk）=0，所以：
而理论上，白噪声的自相关函数只在p=0时取一值即它的方差σ2N，而在其他地方均为0，于是：
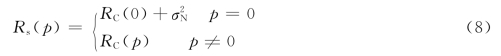
式中，因为噪声分量只在p=0点有值，是自相关整个序列所表现出来的特征。从这个意义上讲，式（8）已经不再受噪声部分的影响，很好地实现了除噪效果。由式（3）可知，有用信号{Ck}其自相关序列RC（p）具有与有用信号{Ck}同样的周期，且各频率成分的振幅为有用信号{Ck}相同频率成分振幅平方的一半。这在水电机组故障诊断中是很有意义的。一个含有噪声和有用信号的故障信号，经过自相关处理，变成了单纯的有用信号成分。分析有用信号得到故障的特征信息，从而为准确地判断故障原因提供依据。故障信号分析时具体步骤如下：
（1）计算故障信号序列的自相关函数Rs（p）。
（2）对自相关函数Rs（p）进行快速FFT变换计算出各频率成分的幅值f（ω）。
（3）则有用故障信号对应频率的幅值