1.3　目标函数

1.3　目标函数

可逆式转轮的优化设计问题是一个多目标最优化问题，本文从水力设计计算角度，在建立目标函数时主要考虑转轮双向流动的综合能量性能和综合空化性能，利用本文中建立的可逆转轮双向流动及设计计算数学模型，就可以获得转轮水轮机工况和水泵工况的双向流动信息，对可逆转轮的综合性能进行评价。

引入可逆转轮综合损失系数的概念，可逆转轮良好的能量性能可以用损失系数作为目标函数来描述：

式中：ξT、ξP分别为机组在水轮机和水泵工况下的损失系数。叶栅的损失系数定义为：

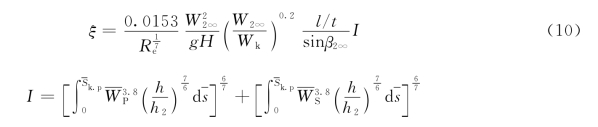
式中，H为水头；t为叶栅栅距；l为翼型弦长；h为研究点流层厚度与原点流层厚度的比值。

对于可逆转轮的空化性能，选取两工况下最大的空化系数作为评价可逆转轮空化性能的综合气蚀系数，即：

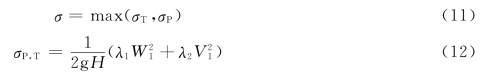
式中，σT、σP分别为水轮机工况和水泵工况下可逆转轮的空化系数；系数λ1和λ2在水轮机和水泵工况下分别取不同的数值。

以转轮的综合空化系数最小和综合损失系数最小的多目标问题为优化模型。选择线性加权的方法，将多个目标转化为一个目标的评价函数，把求解多目标的极小问题归结为求解与之相关的单目标极小化问题，即：

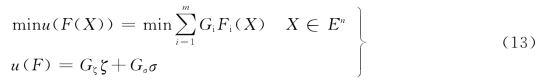
式中：Gi代表了相应目标Fi在模型中的重要程度，Gζ+Gσ=1。若取Gζ=0，Gσ=1，可以得到空化性能最好的转轮；取Gζ=1，Gσ=0，可以得到综合效率最高的转轮。