2.3　网格的划分

网格数量的大小将影响筒体计算结果的精密程度和计算规模的大小。一般来讲，网格划得越细，计算精度会有所提高，同时，网格划得越细，产生的单元数、结点数及自由度数就越多，计算也就变得越复杂，所需的计算机资源、CPU运行时间也就越多。图2描述了计算精度和所耗时间与网格数量的变化图。

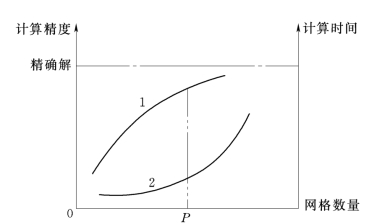
图2　计算精度和计算时间与网格数量关系图

1—计算精度随网格数量的变化；
2—计算时间与网格数量的关系

图中曲线1表示结构中的计算精度随网格数量的变化情况，曲线2代表了计算时间与网格数量的关系。从图中可以看出，当网格数量较少时增加网格数量可以使计算精度明显提高，而计算时间不会有很大的变化。当网格数量增加到一定程度后，再继续增加网格数量，计算精度提高甚微，而计算时间却大幅度增加。图2中P点处的网格数量，使得模型既有比较高的计算精度，同时计算时间又不是太长，因此是比较合理的网格数量。在实际计算中，可以比较两种网格划分的计算结果，如果两次计算结果相差较大，可以继续增加网格，相反则停止计算。本课题经过多次计算，当网格尺寸大小为15mm，公差为0.75mm时，继续减少网格尺寸对计算精度的提高并不明显，但运行时间却显著提高，因此，选用该尺寸进行网格划分。在边界比较曲折、应力比较集中、应力梯度比较大的地方，为了提高计算精度，网格应划得细一些。所得的单元总数为165222，结点数为304679。筒体的网格图如图3所示。