1.2 双向轴流叶轮设计奇点分布法
奇点分布法是轴流式叶片设计常采用的方法，本文S形叶片设计采用的是奇点分布法。它的基本出发点是用一系列分布在翼型骨线上的奇点来代替叶栅中的翼型对水流的作用。用奇点分布法解决无限薄翼型叶栅绕流反问题即绘制骨线的方法是：在选定的旋涡分布规律r（s）的条件下，求出由旋涡层和平面平行来流合成的基本翼型骨线上点的速度分布，利用绕流无分离的条件即翼型上各点的速度向量必须与基本翼型骨线相切的性质来绘制骨线的形状。
用奇点分布法设计轴流泵时给定的基本设计参数有三个，即设计流量Q，设计扬程H和设计转速n。则比转速
可相应得出，根据ns可决定叶片数Z，决定叶轮的轮毂比dh/D。其中，dh和D分别为轮毂直径和叶轮直径。在假定了轴面速度Vm的前提下，可分别计算出dh和D。
将半径为r的圆柱面沿其中一条母线剖开，展开成一平面，得到一个彼此距离相等翼型相同的无穷叶栅，假设叶栅的翼型很薄，骨线是直线，即平板翼型。骨线与翼型的弦线重叠，见图1。已经确定了叶片数Z，而叶栅距
，所以t可求出。每个圆柱面的叶栅稠密度1/t可根据经验公式确定，翼型弦线长度l可知。另外，叶栅前后水流相对速度
都可根据设计流量Q，设计扬程H及设计转速n等计算，由此平面平行来流速度
可知，其值
和来流角度β∞可相应计算出来。而翼型安放角βen=β∞+α，这里α为冲角，一般取2°～3°，所以βen可以计算出来。
如图1所示，u—z坐标系的坐标原点在基本翼型骨线的中点，也是s坐标的原点。沿骨线分布的环量密度r（s），一般取：
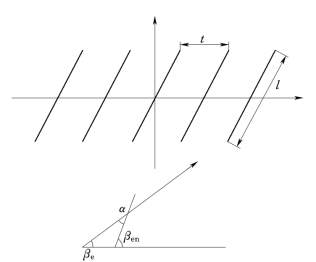
图1 平板叶栅及几何参数
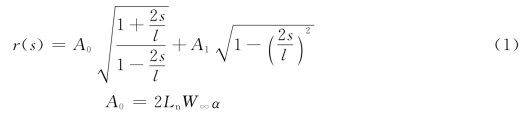
式中，Ln是修正参数，它是叶栅密度1/t和栅轴安放角βen的函数。
旋涡总强度应等于给定的绕骨线环量值ΓB，即：
根据公式ΓB=
可确定：
平面上任意点的速度
，投影到坐标轴上，得：
基本翼型旋涡层引起的诱导速度
可近似的按直线翼型计算，即：
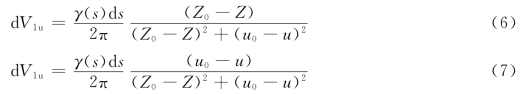
根据势流理论，旋涡层对叶栅中翼型骨线（包括基本翼型）上各点的诱导速度分量分别为：
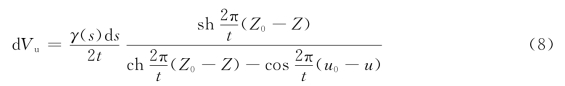
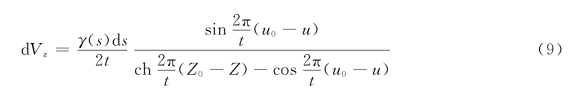
且
积分可得除基本翼型之外所有旋涡层在s0点的速度分量V2u和V2z。
骨线上多个点（一般取7个点）的速度向量Wu和Wz计算出来，半径为r的圆柱面上的骨线就可绘出，于是就可得到翼型的最终骨线形状。
类似正向翼型计算方法，根据反向水泵工况的设计参数可以计算出适合于反向工作的翼型骨线，将正反向翼型的骨线叠加在一起，分别取正反向翼型骨线的进水部分线段即组成正S形骨线。