双向流动优化设计算例
优化计算的转轮相关参数如下：流量qv=57.43m3/s，转速n=500r/min，转轮直径D1=3.85m，水头H=533m，导叶高度b=0.374m，叶片数B=6。
图2和图3所示分别为转轮的轴面流道、厚度分布规律和给定的初始环量分布。
优化计算的有关控制参数如下：初始单纯形步长：
=0.1；优化收敛精度：ε=2×10-3；全三维设计收敛精度：
=5×10-2；流动计算收敛精度：
=5×10-2。
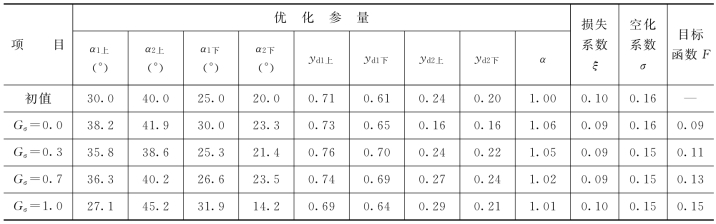
表1所示为分别取权重系数Gσ=0.0、0.3、0.7和1.0四种方案下双向流动优化计算的结果。Gσ由0.0变化到1.0，评价函数从损失系数最小变化至空化系数最小。
由表1中可以看出，以综合损失系数为目标函数，可逆转轮优化计算后为0.086，减小了12.8%；以综合空化系数为目标函数，可逆转轮优化计算后为0.148，减小了4.7%。优化设计可以改善转轮的能量性能和空化性能。
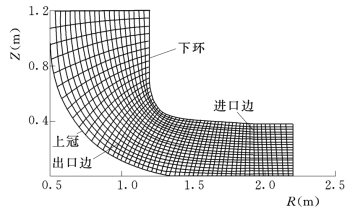
图2 水泵水轮机转轮反问题计算流道图
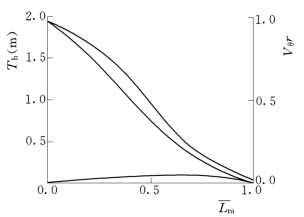
图3 给定的厚度分布规律和初始环量分布
表1 不同权重系数下双向流动优化计算结果
本文仅给出Gσ=0.0和Gσ=1.0的优化计算结果。图4所示为损失系数最小的优化计算结果。其中图4（a）为优化计算的环量分布，图4（b）和图4（c）为叶片的轴面截线和水平截线（图中，实线为正面，虚线为背面）。由图4中可以看出，优化设计的叶片比较光滑。
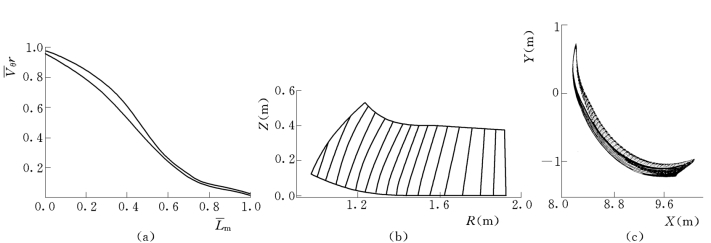
图4 损失系数最小优化计算结果
（a）速度矩分布规律；（b）叶片轴面截线；（c）叶片正背面水平截线
该模型在优化计算过程中可以得到转轮的双向流动信息，图5所示为以损失系数最小优化的可逆转轮内双向的轴面流速分布。由图5中可以看出，可逆转轮内部的双向流动比较光滑。
图6所示为空化系数最小的优化计算结果，在图6（c）中，实线表示叶片的正面，虚线表示叶片的反面。图7所示为优化计算的可逆转轮双向轴面流速分布。
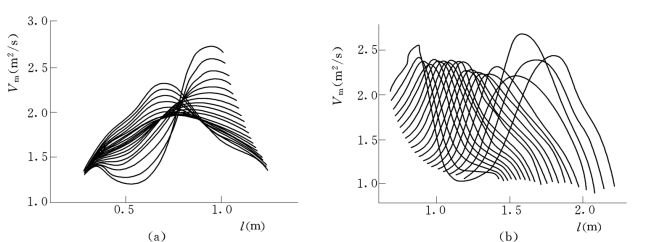
图5 损失系数最小优化计算双向流动
（a）水轮机方向轴面速度分布；（b）水泵方向轴面速度分布
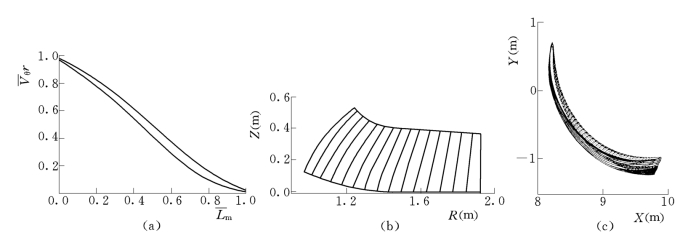
图6 空化系数最小优化计算结果
（a）速度矩分布规律；（b）叶片轴面截线；（c）叶片正背面水平截线
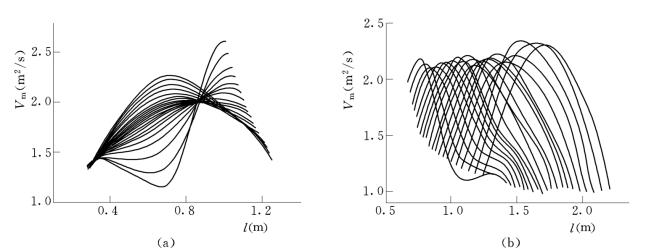
图7 空化系数最小优化计算双向流动
（a）水轮机方向轴面速度分布；（b）水泵方向轴面速度分布
这里仅给出以损失系数最小和以空化系数最小优化计算的结果。比较不同目标函数下的优化结果可以看到，以空化系数最小为目标函数优化的转轮叶片包角较大，较大的包角可以形成较长的流道使水流平稳，叶片单位面积的负荷也小，因而空化系数小；以损失系数最小为目标函数优化的转轮叶片包角较小，包角小，叶片短，摩擦损失小，因而损失系数小。
以损失系数最小和以空化系数最小优化计算的叶片，双向工况下轴面速度的分布均比较光滑，变化也比较均匀。以空化系数最小优化所得的
分布较以损失系数最小优化所得的
分布变化更为均匀，
的分布决定了叶片负荷的分布，因而叶片压力的分布规律也更为平坦。
图8所示的分别为以损失系数最小和以空化系数最小进行优化设计目标函数的收敛过程曲线。由于优化计算是在获取双向流动信息的基础上进行的，优化参量在寻优过程中进行反问题计算得到的不光滑叶片可能导致正问题流动计算出现不收敛的情况，本文在进行双向流动优化计算时，对于上述情况，直接给定目标函数极大值，使得参量的寻优过程返回到正常的范围内进行。
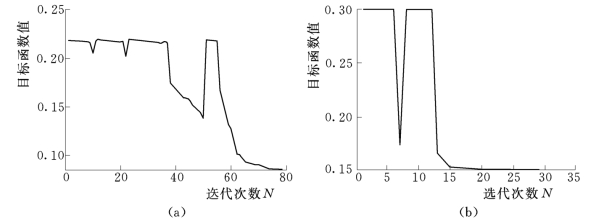
图8 优化过程曲线
（a）损失系数最小；（b）空化系数最小