模型及变量检验
本书中经过因子分析得到的自变量都为数值型变量,因变量公共服务满意度也以数值型变量的方式呈现。基于研究目的和数据类型,采用多元回归分析来确定最终的模型,并检验各自变量(各因子)对因变量(公共服务满意度)的影响极其作用程度。
(一)模型检验
经过逐步回归分析方法,最终确定的模型如方程6-1式所示。经过检验,该模型p<0.01,说明该模型具有显著统计学意义;模型的R2为76.90%,说明模型稳健度较好,但只有六个因子进入了模型(公共文化没有进入模型),选入模型的六个因子可以解释因变量近77%的变异程度。因此,模型通过检验,可靠度较好。
Y=0.006+B1X1+B2X2+B3X”3+B4X4+B5X5+B7X7
…(方程6-1)
(二)变量检验
在此以基本公共服务满意度作为因变量,以七个维度因素值即医疗卫生服务、义务教育服务、基础设施服务、行政服务、社会保障服务、公共文化服务以及公共安全服务等为自变量(入选预测变量),以SPSS19.0为分析工具,对基本公共服务满意度进行多元回归分析,其结果见表6-8。
表6-8 基本服务满意度影响因素的多元回归分析
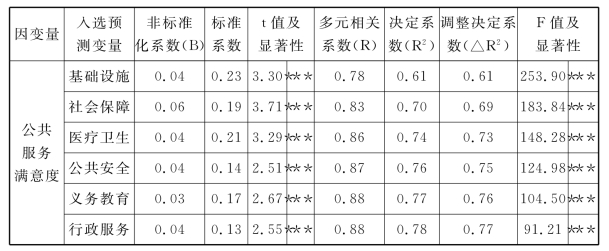
注:***:P<0.001.;回归系数α=0.66
其一,在以医疗卫生服务为自变量的情况下,R2(决定系数)的值为0.74,即以医疗卫生服务为自变量时,有74%的基本公共服务满意度变异量可以得到解释;调整决定系数△R2(增强解释量)说明了预设模型与实际情况的拟合程度,其值为0.73,因此可以看出在医疗卫生服务维度上较为理想的拟合优度;同时,在该情况下的标准回归系数β=0.21,在基本公共服务满意度影响因素中,医疗卫生服务起到了显著的正相关作用。
其二,在以义务教育服务为自变量的情况下,R2(决定系数)的值为0.77,即以义务教育服务为自变量时,有77%的基本公共服务满意度变异量可以得到解释;调整决定系数△R2(增强解释量)说明了预设模型与实际情况的拟合程度,其值为0.76,因此可以看出在义务教育服务维度上较为理想的拟合优度;同时,在该情况下的标准回归系数β=0.17,在基本公共服务满意度影响因素中,义务教育服务起到了显著的正相关作用。
其三,在以基础设施服务为自变量的情况下,R2(决定系数)的值为0.61,即以基础设施服务为自变量时,有61%的基本公共服务满意度变异量可以得到解释;调整决定系数△R2(增强解释量)说明了预设模型与实际情况的拟合程度,其值也为0.61,因此可以看出在基础设施服务维度上较为理想的拟合优度;同时,在该情况下的标准回归系数β=0.23,在基本公共服务满意度影响因素中,基础设施服务起到了显著的正相关作用。
其四,在以行政服务为自变量的情况下,R2(决定系数)的值为0.78,即以行政服务为自变量时,有78%的基本公共服务满意度变异量可以得到解释;调整决定系数△R2(增强解释量)说明了预设模型与实际情况的拟合程度,其值为0.77,因此可以看出在行政服务维度上较为理想的拟合优度;同时,在该情况下的标准回归系数β=0.13,在基本公共服务满意度影响因素中,行政服务起到了显著的正相关作用。
其五,在以社会保障服务为自变量的情况下,R2(决定系数)的值为0.70,即以社会保障服务为自变量时,有70%的基本公共服务满意度变异量可以得到解释;调整决定系数△R2(增强解释量)说明了预设模型与实际情况的拟合程度,其值为0.69,因此可以看出在社会保障服务维度上较为理想的拟合优度;同时,在该情况下的标准回归系数β=0.19,在基本公共服务满意度影响因素中,社会保障服务起到了显著的正相关作用。
其六,以公共安全服务为自变量的情况下,R2(决定系数)的值为0.76,即以公共安全服务为自变量时,有76%的基本公共服务满意度变异量可以得到解释;调整决定系数△R2(增强解释量)说明了预设模型与实际情况的拟合程度,其值为0.75,因此可以看出在公共安全服务维度上较为理想的拟合优度;同时,在该情况下的标准回归系数β=0.14,在基本公共服务满意度影响因素中,公共安全服务也有较为显著的正相关作用。
同时,公共文化这一因素没有成为公共服务满意度这一因变量的自变量,即公共文化这一因素没有进入公共服务满意度的回归方程,说明在控制其他变量的情况下,公共文化这一因素对因变量基本公共服务满意度没有统计学意义。
经过以上分析,我们最初建立的基本公共服务满意度的估计方程,以及将基本公共服务满意度设为Y,则有:公共服务满意度(Y)=0.66+0.04医疗卫生(X1)+0.03义务教育(X2)+0.04基础设施(X3)+0.04行政服务(X4)+0.06社会保障(X5)+0.04公共安全(X7)。
Y=0.66+0.04X1+0.03X2+0.04X3+0.04X4+0.06X5+0.04X7
…………………………………………………………(方程6-2)
是完全符合现实并且成立的。回归方程的整体有效程度,一般情况下可通过方差分析来完成。我们在表6-8中看到的F值及其显著性就是方差分析的结果,所有引入方程的六个维度的F值的相伴概率均为0.000,这个数值远远小于0.05。因此说明,无论是医疗卫生服务,还是义务教育、基础设施、行政服务、社会保障以及公共安全,对公共服务满意度有显著影响。
