1.2　弹性分析的数值解法

勒夫（A.E.H.Love）（1944）在其经典著作《A Treatise on the Mathematical Theory of Elasticity》中首先指出：“数学弹性理论致力于研究某一受平衡力系作用或处于轻微的内部相对运动状态下的固体，试图把它的内部应变或相对位移纳入计算，并努力为建筑、工程以及所有构造材料为固体的工艺方面，求得实用上重要的结果。”这似乎已经成为弹性理论的一个标准定义。

弹性理论对于应力、应变和位移这些物理量，通过几何学、物理学和静力学的分析，建立了这些变量需要满足的弹性域内控制方程（一般表达式多为偏微分方程组的形式），根据弹性域所受外力与边界约束状况确定问题的定解条件。

而其求解方法可大致分为两大类：其一，对于各类给定的问题，求解上述控制方程，得到各个物理量在弹性域内的连续函数解，即解析解（精确解），这类方法称为解析解法。然而，虽经数学、力学工作者长期的努力，也只是对少数几何形状规则、荷载与边界比较简单的问题得到了解答。对于多数问题，尤其是在工程实际问题中，当弹性域或者边界条件较为复杂时，通常难以得到解答。其二，为此，对已建立的微分方程需要寻求近似解法——数值解法。

在弹性力学问题中，变分法是被广泛应用的数值解法之一。

变分法是将待求函数应满足的一定的微分方程和定解条件这样的提法变为待求函数是一定的泛函（函数的函数）的极值函数，也就是说，令泛函取极值的函数就是微分方程的解。用这种方法寻求近似解，首先要针对给定问题推导出相应的泛函，泛函一般表达式为求解区域内的定积分形式；然后设出待求函数（在泛函中包含的函数）的试探函数，试探函数中包含已知的函数系列和系列中每个待求系数；把试探函数代入泛函，对其中的已知函数进行运算后，泛函中未定的也只有各个待定系数，泛函也就变成了待求系数的多变量函数了，泛函的极值问题就变成了函数的极值问题；利用多变量函数求极值点的条件可以推导出求待定函数的代数方程组。

变分法在弹性力学问题求解中曾成功得到了应用，但因其对工程中几何形状和边界条件较为复杂的各种问题仍难以得到解答，因而未能在工程问题中得到广泛应用。自20世纪70年代以来，依托电子计算机的高速发展和普及而迅速发展的有限单元法，则很好地弥补了上述方法的缺陷，极大地推动了数值计算的应用。

图1.1给出了弹性分析的主要方法。

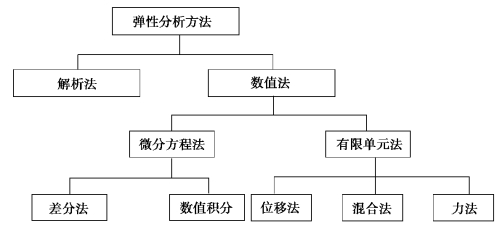
图1.1　结构分析常用方法