▶8.2.1　局部坐标系中的单元刚度矩阵

▶8.2.1　局部坐标系中的单元刚度矩阵

弹性薄壳的应力状态可以认为是平面应力状态和弯曲应力状态的组合。因此，薄壳单元的刚度矩阵也可以由这两种应力状态的刚度矩阵加以组合而得到。参阅图8.4，把局部坐标系的x轴和y轴取在单元所在平面内。

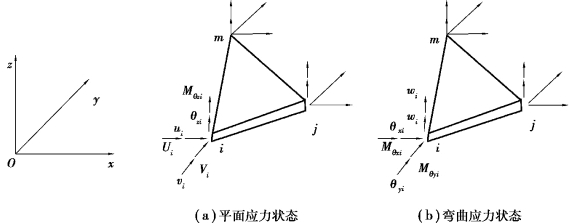
图8.4　薄壳单元的结点力和结点位移

对于平面应力状态，由第2章可知，单元的应变状态完全取决于各结点的位移u和v，以三角形单元为例，单元的等效结点荷载与结点位移的关系如下：

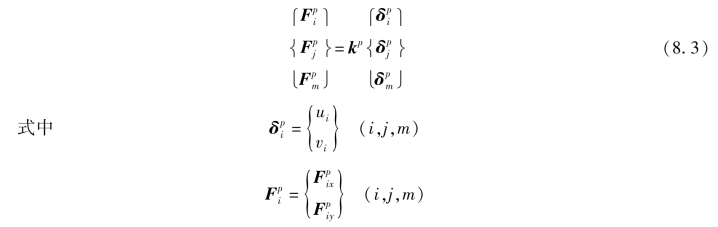
结点转角θzi，θzj，θzm不影响结点力，可以不考虑，相应的结点力也不存在。

对于弯曲应力状态，单元应变状态取决于结点在z方向的线位移w，绕x轴转角θx及绕y轴转角θy，结点力和结点位移的关系如下：

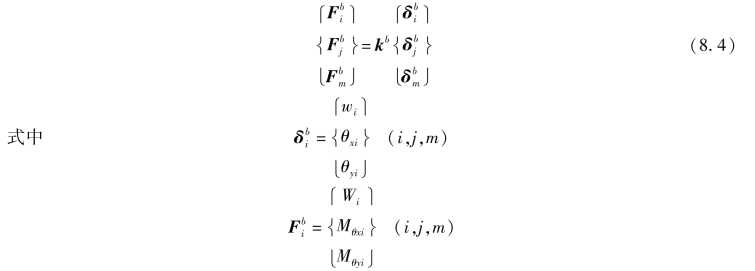
把平面应力与弯曲应力加以组合后，单元的结点位移和结点力如下：

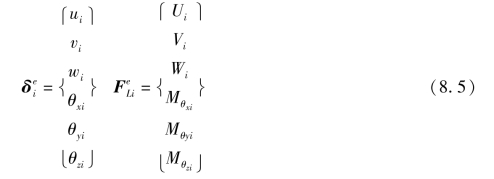
虽然转角θzi不影响单元的应力状态，为了便于以后将局部坐标系的刚度矩阵转化为整体坐标系的刚度矩阵并集合成整体刚度矩阵，我们特地将θzi也包括在结点位移中，并在结点力中相应地包括一个虚拟弯矩Mθzi。

单元的结点力与结点位移的关系可写成

可表示为

式中　k——在组合应力状态下的单元刚度矩阵。

由于平面应力状态下的结点力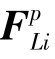与弯曲应力状态下的结点位移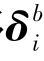互不影响；弯曲应力状态下的结点力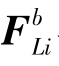与平面应力状态下的结点位移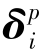也互不影响；所以组合应力状态下的单元刚度矩阵k的子矩阵可以写成如下形式：

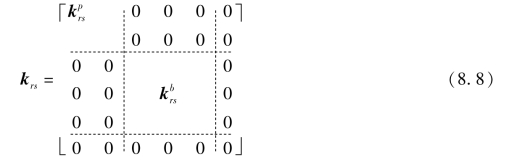
式中　——分别为平面应力问题和薄板弯曲问题的相应子矩阵。

因此，把平面应力问题和薄板弯曲问题中三角形单元刚度矩阵结合起来，即可得到组合应力状态下三角形单元的刚度矩阵，如图8.5所示。对于矩形薄壳单元，这种组合方法也是适用的，只是刚度矩阵是24×24阶的。

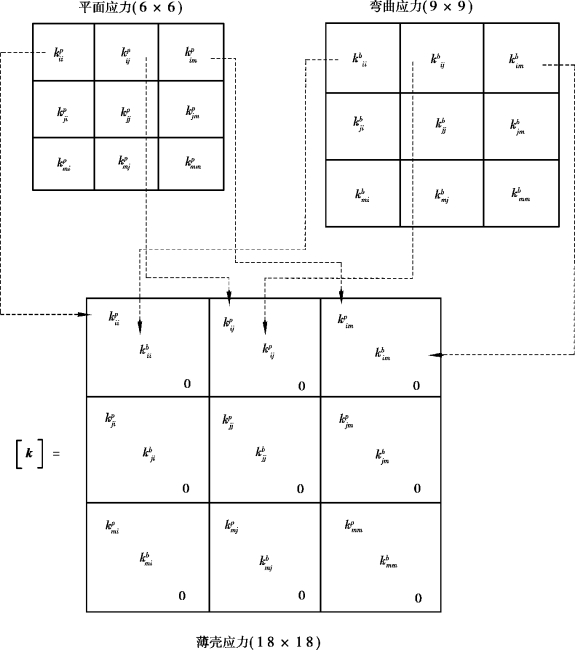
图8.5　由平面应力和薄板弯曲的刚度矩阵组成薄壳单元刚度矩阵