▶2.1.1 单元划分
假想把连续弹性体分割成若干个有限大小的单元，单元之间仅在结点处相互连接。这种仅在结点连接，仅靠结点相互作用的集合体，称为单元集合体。
从理论上说，单元划分具有一定的任意性，但在实际计算中必须根据研究对象的特点，使单元划分既满足力学分析要求，又能够达到计算高效的目的。因此，为便于计算，单元的几何形状一般采用简单形式。例如，对于平面问题单元的基本形式取为三角形与四边形，三维空间问题单元的基本形式为四面体和六面体（图2.1）等。
图1.2所示平面弹性域，采用三角形单元进行划分，在边界上“以直代曲”，即采用折线来近似取代原曲线边界。这种几何形式带来的误差将通过“细分”来减小。实际上，在一定条件下，随着这种逐渐细分，其极限状态趋向于实际曲线。
这种思想可追溯到古代，例如，古希腊的数学家和物理学家阿基米德就在面积、体积的计算方法中引入了分割取代的方法；公元3世纪我国的数学家刘徽在其著作《九章算术注》中也提出了割圆术，即离散原理：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”换言之：离散越细，误差越小。正如，方砖可以砌成圆井，直锯可以锯出曲板，任意的连续曲线或曲面都可以分割成许多小段或小块。
（1）单元类型
根据所分析问题的类型，常用的结构分析单元类型通常分为：①杆/桁架单元；②梁单元；③平面单元；④薄板单元；⑤薄壳单元；⑥一般三维应力单元等。此外，还有一些应力状态较为特殊的结构分析单元，如索单元、膜单元、管单元、厚板单元、厚壳单元等。
图2.1给出了一些从几何特征上分类的平面问题和三维应力问题常用单元。
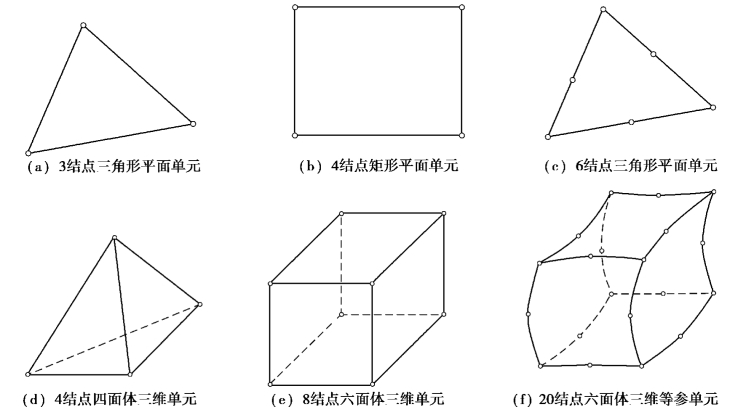
图2.1 平面问题和三维应力问题常用单元
（2）结点类型
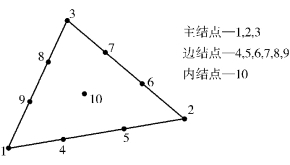
在有限元法整体结构中，将单元与单元之间设置的相互连接点，称为结点。一般用数字1，2，…表示结点编码。在单元区域内的编码称为单元局部编码（图2.2）。在位移解法有限元法中，取结点广义位移为结构的自由度，以此来决定相邻单元公共结点的连接方式。结点的设置、性质及数目等，视所求解问题的性质、描述变形状态的需要和计算精度的要求而定。
单元结点设置一般分为主结点（顶点或角点）、边结点和内结点等3类（图2.2）。
图2.2 10结点三角形平面单元
对于只有平动自由度的问题，单元结点应具有平动自由度，类似于铰连接，因此，结点取为铰结点，例如桁架、平面问题、三维实体问题等。对于具有平动和转动自由度的问题，单元结点则具有平动和转动自由度，结点取为刚结点，例如梁、板、壳等问题。
在有限元法中引进结点概念是至关重要的，设置结点，可将实际连续体看成是仅在结点处相互连接的单元群组成的离散型结构，从而可使整体结构将以结点位移参数作为基本未知量，进而通过其进行应力、变形分析。
实际上，相邻的单元在整个公共边界处（包含结点）均是相互连接、相互作用的，而离散模型设定除结点外，均不相互连接和相互作用，这一点与实际状态不相符。因而，在单元分析中要求设置的位移函数在公共交界处变形协调（具体方法将在单元分析一节中阐述），从而使得离散模型反映实际受力与变形状态的目的。另一方面，随着单元网格的逐渐细分，其极限状态趋近于实际状态。
下面通过实例来说明建立有限元离散模型的具体方法与过程。
如图2.3（a）所示为一深梁构件，不计自重，将其简化为平面应力问题。根据对称性取其
模型进行分析[图2.3（b）]。
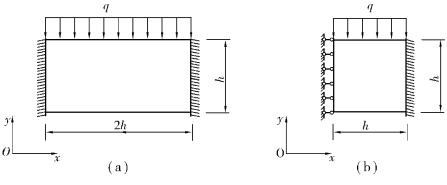
图2.3 平面应力问题
采用3结点三角形平面单元，对图2.3（b）所示结构进行划分。整体结构划分为8个单元，结点为铰接。共计设置9个结点，18个自由度，如图2.4（a）所示。
图2.4（b）为采用4结点矩形平面单元对结构进行划分。整体结构划分为16个单元，共设置25个结点，50个自由度。
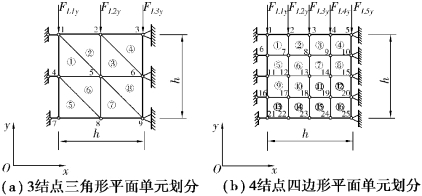
图2.4 结构离散分析模型