▶2.2.5 单元基本方程和单元刚度矩阵
最小势能原理可表述为：在所有满足变形协调和边界条件的位移函数中，真实的位移函数使得弹性体的总势能取驻值，进一步的分析表明，该驻值为极小值。简言之，在一切变形可能的状态中，真实位移所产生的弹性体总势能取最小值。
（1）弹性体系的总势能的一般表达式
在能量守恒的前提下，任意弹性体系的总势能Πs为总应变能U与外力势能V之和，即
式中 U——弹性体应变能；
V——弹性体外力势能。
根据弹性理论，弹性体中任一微元体的应变能为
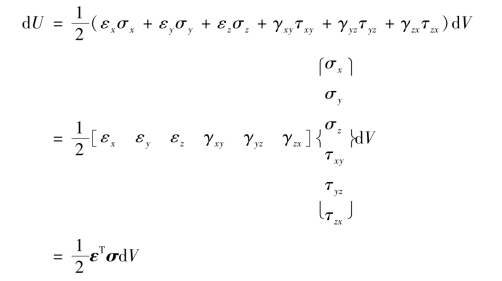
则弹性体应变能可表达为
由物理方程（1.16），可得
根据能量原理，弹性体在变形过程中，外力做功使得弹性体外力势能减小。设W为弹性体变形过程的外力所做的功，根据能量守恒原理，则外力势能为
式中 f——弹性体承受的体力；
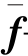——弹性体承受的面力。
因此，弹性体总势能的一般表达式可写作
（2）单元基本方程
在单元分析中，设U为单元应变能。将式（2.20）和式（2.23）代入式（2.28），得到单元应变能
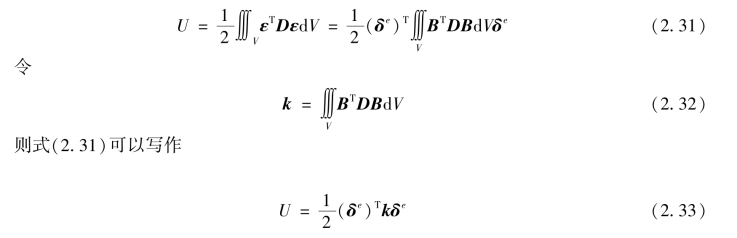
单元变形过程中外力做功使得单元外力势能减小，此时单元仅承受单元结点力Fe作用。根据能量守恒原理，则外力势能为
单元总势能可表达为
可见，单元总势能是单元结点参数δe的泛函，根据最小势能原理可得
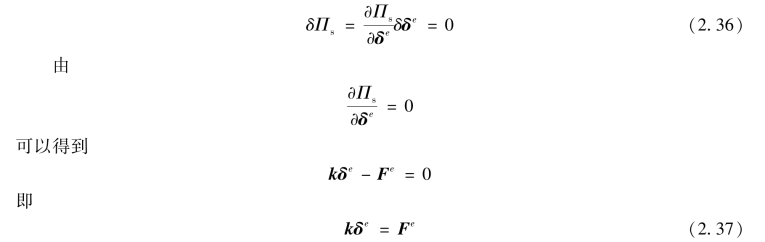
式（2.37）为单元基本方程，其中k称为单元刚度矩阵，简称单刚。
上述利用最小势能原理推导单元基本方程的过程及表达式具有一般性。
（3）单元刚度矩阵
由式（2.32）可知，由于kT=k，因此单刚k为对称矩阵。
对于厚度为常数t的3结点三角形平面单元，单刚k可简化为
根据式（2.1）～式（2.4），将单刚k表示为对应于结点的分块形式
于是，式（2.37）可以写作
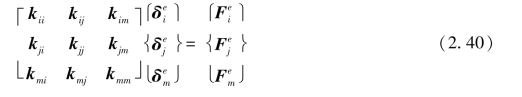
其中子块为
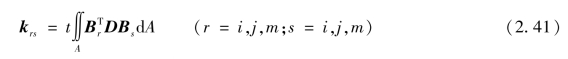
式中 krs=（r=i，j，m；s=i，j，m）分别应于单元结点r，s。
对于3结点三角形常应变单元，B，D均为常数阵，因此式（2.38）可进一步简化为：
图2.7给出了各物理量应力σ、应变ε、位移u与单元结点位移δe、单元结点力Fe之间的逻辑转换关系。
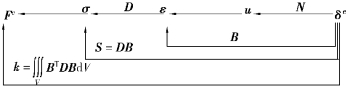
图2.7 各物理量之间转换关系