▶9.2.2　集中质量矩阵

▶9.2.2　集中质量矩阵

由式（9.9）集合得到的整体质量矩阵M将是带状的对称矩阵，其计算存储数据量与刚度矩阵K相同。为了简化计算，假设单元的质量集中分配在各结点上，这样得到的质量矩阵是对角线矩阵，称为单元集中质量矩阵。于是，整体质量矩阵M也将是对角线矩阵，给存储和计算都带来了方便。

动力方程（9.13）可以由拉格朗日方程推导出，其中结构的总动能就是各单元动能之和，即

单元内位移由结点位移插值为

则速度为

如ρ为材料密度，则单元动能为

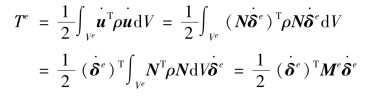
可见，单元动能为结点速度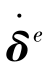的二次型，而单元质量矩阵就是此二次型的系数矩阵。

对于平面或三维问题，结点位移部分为互相垂直的线位移，如果把单元的质量平均分配到单元各结点，则单元动能为

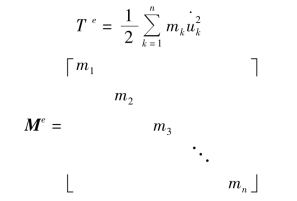
其中，mk为对应于k号结点位移分量的结点质量，n为单元自由度数，这样的质量矩阵就是对角型的，有

例如，对3结点三角形平面单元，单元总质量为M，每结点都集中有平均分配的质量。此单元有6个自由度，则其中单元集中质量矩阵为

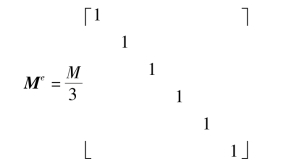
而4结点四面体单元的自由度为12，M为单元总质量，则此单元的集中质量矩阵为

其中I为12阶单位阵。

对于直梁与板壳，动能计算较为复杂，而按式（9.9）仍可求得其一致质量矩阵。但是，为了简化计算，也可以直接将单元质量平均分到各结点，成为几个质点，得到集中质量矩阵。例如，两结点直梁单元，i，j为两结点，M为单元质量。如果把质量平均分配并集中到两个结点，而对应的单元结点位移为

则动能为

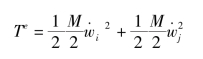
集中质量矩阵为

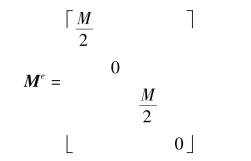
其中零对角元素对应于两结点的转动位移θi，θj。因为质量集中于两个质点，也就忽略了梁截面转动的惯性。对于细梁和薄板壳，对应于结点转动的动能是很小的，一般都可以忽略。只把单元质量分配到各结点，最为质点只计算线位移运动的动能而得到单元的集中质量矩阵，这是合理的，又较为简单。