▶8.2.2 坐标转换、整体刚度矩阵
前面是在单元的局部坐标系中推导单元刚度矩阵的，即以单元的中面为xy面，z轴垂直于单元的中面。为了建立薄壳的整体刚度矩阵，必须把不同平面内的单元刚度系数在结点处加以集合，因此需要另外确定一个统一的整体坐标系，并把各单元在局部坐标系中的刚度矩阵转换到整体坐标系中去。
现在用x＇，y＇，z＇表示整体坐标，局部坐标仍用x，y，z表示。在局部坐标系中，结点i的位移和结点力仍用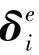
和
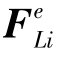表示，见式（8.5）。在整体坐标系中，结点i处的位移和结点力用
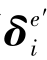和
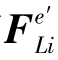表示，即
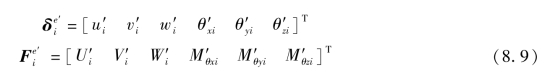
结点位移和结点力在2个坐标系中（图8.6）的变换可按下式进行：
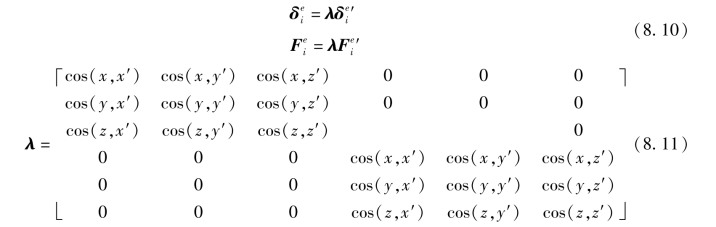
而（x，x＇）为x轴与x＇轴的夹角，等等。
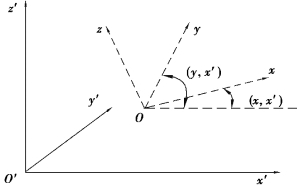
图8.6 局部坐标系（x，y，z）与整体坐标系（x＇，y＇，z＇）
把整个单元在整体坐标中的结点位移和结点力分别用（δ＇）e及（F＇）e表示，由变换式（8.10）可得到
由式（8.12）的第二式可知
把局部坐标中单元结点力与结点位移的关系式Fe=kδe代入上式，得
可见L-1kL就是此单元在整体坐标系中的刚度矩阵，即
因L是正交矩阵，故L-1=LT，由上式可得
这就是刚度矩阵的变换公式，利用这个公式，可以由局部坐标中的单元刚度矩阵k计算整体坐标中的单元刚度矩阵k＇。
将刚度矩阵写成分块形式，k＇的子矩阵可按式（8.15）计算：
式中 krs——按式（6.6）在局部坐标中计算的。
当整体坐标系中的单元刚度矩阵计算出来以后，按照以前所述统一步骤，加以集合，不难得到壳体的整体刚度矩阵K。
为了建立结点平衡方程，还需计算结点等效荷载。令单元荷载所做的功等于结点等效荷载所做的功，不难求出单元结点等效荷载。一般情况下，在分布荷载作用下，单元结点等效荷载包括力和力矩分量。实际上，当单元比较小时，常可采用比较简单的方法计算单元结点等效荷载，即忽略力矩分量，并把单元承受外荷载的合力平均分摊到单元的各结点上去。例如，当壳面承受着法向分布荷载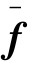
，在三角形单元3个结点上的荷载强度分别是
，那么作用于单元上的荷载的合力为
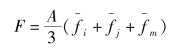
式中A是单元面积，假定荷载方向与局部坐标z轴相同时为正。把这个合力平均分摊到3个结点上，并转换到整体坐标中去，得到在整体坐标中的结点荷载如下：
其中x＇y＇z＇是整体坐标系。将各单元的结点荷载加以集合，即可得到壳体的荷载列阵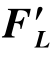
。壳体的结点平衡方程为
从式（8.17）可解得各结点在整体坐标系中的位移。利用变换式δe=L（δ＇）e求出各结点在局部坐标系中的位移，再利用局部坐标系中的应力矩阵，即可求得各单元的应力。
有一个特殊情况必须注意。如果交会于一个结点的各单元都在一个平面内，由于在式（8.8）中已令θzi方向的刚度系数等于零，在局部坐标系中，这个结点的第6个平衡方程（相当于θz方向）将是
如果整体坐标与这一局部坐标一致，显然，整体刚度矩阵的行列式|K|=0，因而式（8.17）不满足有唯一解的条件。如果整体坐标与局部坐标不一致，经过变换后，在这个结点得到了表面上正确的6个平衡方程，但是由于式（8.18），行列式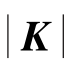
的行向量是线性相关的，从而|K|=0，所以平衡方程（8.17）仍然不满足有唯一解的条件。
为了排除这一困难，对于这种各有关单元位于同一平面内的结点，可以在局部坐标系内建立结点平衡方程，并删去θz方向的平衡方程0=0，于是剩下的方程组满足有唯一解的条件。这个方法在程序设计上比较麻烦。
另一个办法是，在这些特殊结点上。给以任意的刚度系数kθz，因此在局部坐标系中，这个结点在θz方向的平衡方程为
经过坐标变换，在整体坐标中的结点平衡方程将满足有唯一解的条件。在解出的结点位移中包括θzi。由于θzi不影响单元应力，并与其他结点平衡方程无关，所以实际上可以给定任意的kθz值而不会影响计算结果。