▶6.1.4 单元刚度矩阵
令单元的结点虚位移
，单元虚位移函数采用与单元位移函数相同的形式，即分别取单元虚位移函数u*和单元虚应变ε*为
其中，N和B分别为形函数矩阵和应变矩阵，分别见式（6.6）和式（6.9）。
根据虚位移原理，当发生约束允许的任意微小的虚位移时，外力在虚位移上所做的虚功等于单元的应力在虚应变上所做的虚功。
令单元的结点力为
，以列阵表示，则为
外力在虚位移上所做的虚功为结点力与相应的结点虚位移
的乘积，即
单元应力在虚应变上所做的虚功为
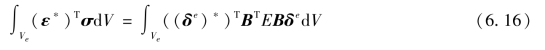
式中 Ve——单元体积。
根据虚位移原理，可得
因为虚应变是任意的，所以，为使上式成立，等式两边与（（δe）*）T相乘的部分应该相等，即
若记
则式（6.19）可以表示为
这就是表示单元结点力与结点位移关系的单元刚度矩阵方程，而k就是单元刚度矩阵。因为对于杆单元，dV=A dx，所以
式中 L——单元长度。
将式（6.9）代入式（6.21），便可得到单元刚度矩阵的显式表示式
由上述分析看到，2结点杆单元的单元应变、应力都是常数。单元刚度矩阵元素也是常数。每个矩阵元素的物理意义与前几章的单元相同，即任一元素kij表示，当第j个结点位移方向上产生1单位的位移，而其他结点位移皆为0时，需要在第i个位移方向上施加的结点力的大小。例如，对于图6.1所示的杆单元，式（6.22）中的元素k11表示当结点1产生1单位的位移而结点2位移为0时，需要在结点1上施加的结点力为（EA）/L，这正是直杆的轴向线刚度。刚度元素分正负，这也是容易理解的，比如k12表示当结点2产生1单位的位移而结点1的位移为0时，需要在结点1上施加的结点力为-（EA）/L，即在结点2上产生一个正的单位位移，要使结点1保持不动，那么就要在结点1上施加负方向的力。杆单元刚度矩阵的物理意义是很容易理解的，如果说前面对二维、三维单元刚度矩阵的物理意义理解欠深刻的话，那么现在通过杆单元的推导就应该很清楚了，因为它们的物理意义是相同的。