▶7.2.3 位移解答的收敛性
（1）刚体位移
由式（7.5），单元位移函数为
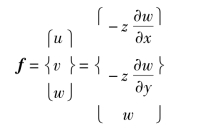
且中面各点处有u=v=0，故薄板所产生的刚体位移只有沿z方向的平动和绕x和绕y轴的转动。由式（7.20）第一项w=a1，这时单元任一点的挠度w是一常量a1，表明单元处于刚体移动状态。第二项w=a2x，这时θy=-
=-a2，单元任一点绕y轴的转角θy是一常量（-a2）。第三项w=a3y，这时θx=
=a3，单元任一点绕x轴的转角θx是一常量a3。因此，位移模式反映了单元刚体位移。
（2）常应变
由式（7.20）中的二次项得板中面变形
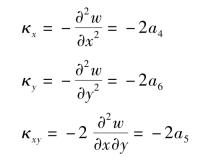
表明单元位移模式反映了常应变。
综上，4结点矩形薄板单元满足完备性要求。
（3）连续性
以图7.5中的边界1—2为例，讨论相邻单元在公共边界的连续性。
在1—2边界上，y=-b=常量，代入式（7.20），可知边界上的挠度w是x的三次函数：
在边界上设置了两个结点1和2，共4个参数，即结点1的挠度为w1，切线转角为θy1=
，结点2的挠度为w2，切线转角为
。利用这4个结点条件完全可以唯一确定式（g）中的4个系数c1，c2，c3，c4。位移模式能够保证相邻单元在公共边界上切线方向挠度及转角的连续性。
下面考察相邻单元边界1—2法线方向的连续性。将y=-b=常量代入式（7.20）第一式，可知边界上的法线转角θx也是x的三次函数：
但是，对于θx来讲，总共只有两个结点条件，即结点1和2的法线转角参数为θx1和θx2，利用这两个端点条件并不能完全确定式（b）中的4个系数d1，d2，d3，d4。
因此，尽管两个相邻单元在公共结点1、2的法线转角彼此相等，但由于两个端点条件不足以确定4个系数d1，d2，d3，d4，因而两个单元在公共边界上的法线转角方程（b）不一定彼此相同，也就是说，在公共边界上的法线转角有可能出现不连续的现象。
综上所述，4结点矩形薄板单元为完备非协调单元。实际上通过其他方法是可以证明该单元的收敛性的。