▶4.3.2 轴对称单元
采用有限单元法求解时,一般采用的单元是轴对称的整圆环,它们的横截面(与rz轴相交的截面)一般采用三角形,例如图4.12中的△ijm,也可以是其他类型的单元。为了简便起见,这里只讨论三角形单元。各个单元之间系用圆环性的铰相互连接,而每个铰与rz面的交点就是结点,例如i,j,m等。这样,各单元将在rz面上形成三角形网格,就像平面问题中各三角形单元在xy面上形成的网格一样。
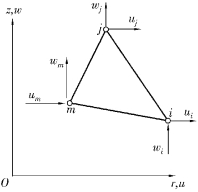
图4.12 轴对称问题三角形环单元
(1)单元位移模式
仿照平面问题,取线性位移模式

得到与平面问题中相似的插值函数,即
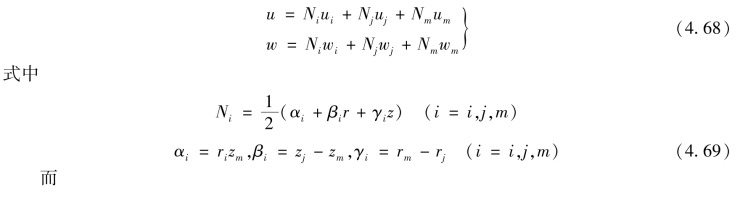
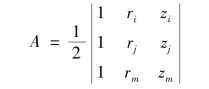
插值函数式(4.55)可以写成矩阵形式
![]()
式中
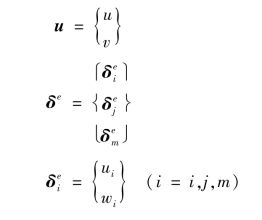
(2)应力应变
将式(4.55)代入轴对称问题的几何方程,得出用结点位移表示单元应变的表达式
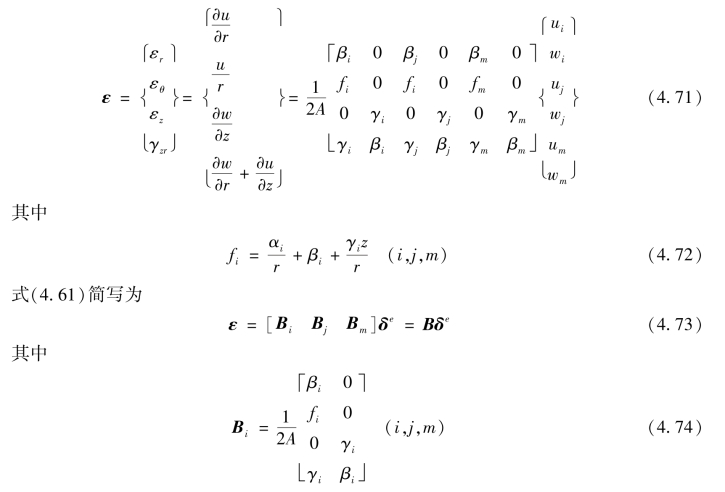
由式(4.64)可见,应变分量εr,εz,γzr,在单元中是常量,但环向正应变εθ不是常量,因为它与公式所示的各个fi有关,而各个fi是坐标r和z的函数。为了简化计算,也为了消除对称轴上由r=0所引起奇异性的麻烦,把每个单元中的r及z近似地用单元中心点的坐标代替,
取为
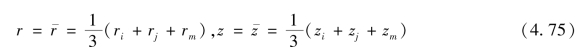
这样也就把各个单元近似地当作常应变单元
单元中的应力表示成为
![]()
则应力矩阵可以表示为
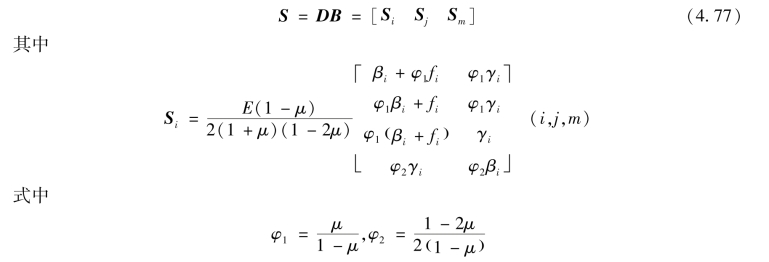
(3)单元刚度矩阵(https://www.daowen.com)
建立单元刚度矩阵时,为了避免非常复杂的积分运算,也将采用简化问题的公式。这样,每个单元中的应变及应力都成为常量,则轴对称问题的单元刚度矩阵为
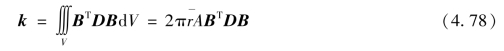
将单元刚度矩阵写成分块形式
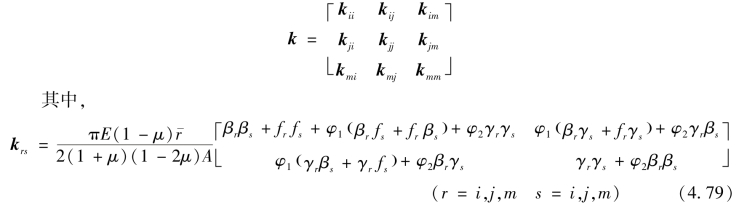
(4)单元等效结点荷载
对于单元体力f=[frfz]T,单元结点荷载列阵为
![]()
对于分布面力![]() ,单元结点荷载列阵为
,单元结点荷载列阵为
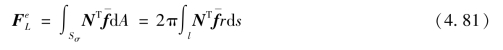
【例4.1】 在体力为自重的情况下,有fr=0而fz=-ρ,其中ρg是容重。于是有
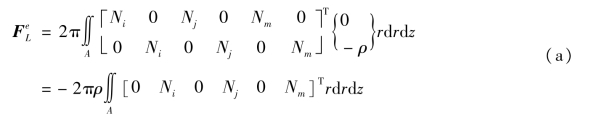
和在平面问题中一样,可以利用面积坐标并建立关系式
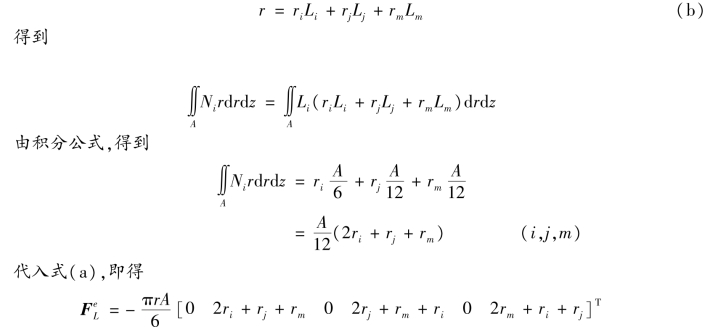
如果单元离对称轴较远,可以认为ri,rj,rm大致相等,则由上式得出简单的结果:可将1/3自重移置到每个结点。
【例4.2】 设在ij边作用线性分布的径向面力,如图4.13所示,则有![]() ,于是由上式可得
,于是由上式可得
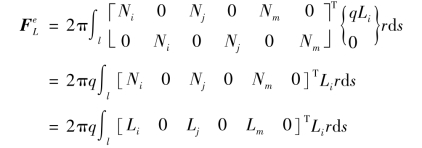
将式(b)代入,并注意ij的边上Lm=0,即由上式可得
![]()
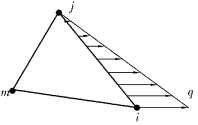
图4.13
应用积分公式,即得
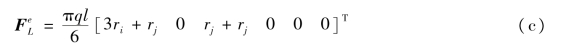
如果单元离对称轴较远,可认为ri与rj大致相等,则由上式得出简单的结果:可将面力合力的2/3移置到结点i,1/3移置到结点j。
有了单元刚度矩阵和单元荷载列阵的计算公式,就可按照前述方法装配得到整体刚度矩阵和整体荷载列阵。
