▶3.3.3　12结点矩形单元（三次单元）

▶3.3.3　12结点矩形单元（三次单元）

图3.10所示为12结点矩形单元，在4个角结点和各边三分点设置2个结点，每个单元有24个自由度。单元结点位移列阵和单元结点力列阵分别为

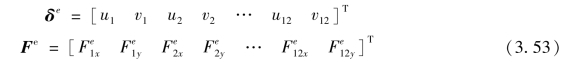
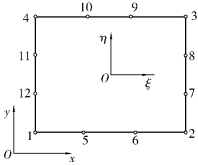
图3.10　12结点矩形单元

参照前述分析过程，单元位移模式为取为

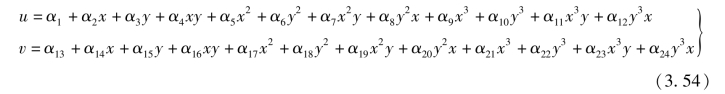
式（3.54）为不完全4次多项式，单元位移模式包含完全的一次项，满足完备性要求。同前述分析，在任意边界上位移函数均为x或y的三次函数。单元各边界均包含4个结点，可唯一确定三次函数，能够保持相邻单元公共边界上位移的协调性，因此该单元为完备协调元。

单元位移插值函数为

按照前述方法，可构造形函数Ni为

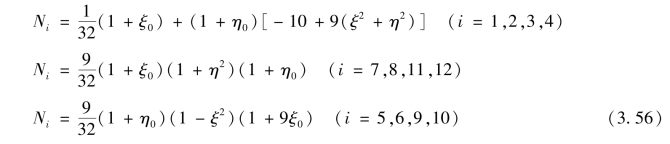
式中，ξ0=ξiξ，η0=ηiη

单元刚度矩阵和单元等效荷载的计算可参照式（3.47）和式（3.48）。

本章主要介绍了常用的三角形和矩形平面单元的构造，从理论上按照上述方法尚可进一步构造更高阶次的单元，但对于结构分析而言，提高计算精度的方法并非仅依靠单元的精度，因此更高阶次的单元已无较大实用意义。

需要进一步说明的是，本章讲述的矩形单元为Serendipity单元（或称索氏单元），有限元分析中通常采用的单元还包括Lagrange单元，Hermite单元等。与其他各类单元相比，索氏单元的特点是在相同数目情况下，结点仅需（或大多）设置在边界上，从而较大地提高了计算效率，因此目前索氏单元被广泛应用。