▶2.3.6 位移边界条件处理
第2.3.2节已建立了以结点位移参数为基本未知量离散体结构分析方程（2.48），该方程是采用有限单元法求解结构弹性问题的基本方程。现在首先考察求解结构弹性问题的解答。
在建立离散结构分析方程的过程中，采用了几何方程、物理方程和最小势能原理。研究表明，应用最小势能原理等价于采用弹性力学基本方程中的平衡微分方程和应力边界条件。这表明，求解结构弹性问题的定解条件（第1.5.5节）中，位移边界条件尚未得到满足，因此应当处理位移边界条件。
另一方面，为消除总刚K的奇异性，亦需要引入位移边界条件，对总刚和整体结点荷载列阵进行修正。
常见位移边界条件一般分为两种，即固定约束边界条件（刚性边界条件）和已知位移边界（非零边界条件）。本书仅针对固定约束边界条件讲述。
处理位移边界条件通常采用两种方法，即主元改1法和主元乘大数法。本节仍以图2.13所示结构为例，说明其使用其方法。
（1）主元改1法
在结构分析方程（2.48）中，如果已知与第i个方程对应的广义结点位移（即整体结点荷载列阵第i个广义结点位移参数）为零，则将整体刚度矩阵K中该行主对角元素Kii改为1，该主元所在的行和列的其他均元素改为0；同时，将整体荷载列阵FL中对应的元素改为0。
由图2.13可知，整体结构位移边界条件为
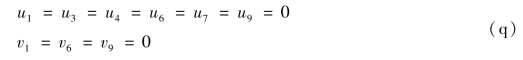
以u4=0为例，说明其具体方法。对整体刚度矩阵K和整体荷载列阵FL作如下修改
考察方程组（r）第7式，可以得到u4=0的结果。对式（q）中其他位移边界条件均做类似处理，即可满足全部位移边界条件。
（2）主元乘大数法
在结构分析方程（2.48）中，如果已知与第i个方程对应的广义结点位移，则将整体刚度矩阵K中该行主元素Kii乘上一个大数（通常大于1010），其他元素不变；同时，将荷载列阵FL中对应的元素改为该为0。
仍以式（q）的边界条件中u4=0为例，对整体刚度矩阵K和整体荷载列阵FL作如下修改
考察方程（s）第7式
由于上式中其他元素比之于主元素K77×1015皆为高阶微量，可以略去。因此，上式仍然可以得到u4=0的结果。
完成了对整体刚度矩阵和整体荷载列阵的修正，可以得到修正后的整体分析方程
式中 
——分别为修正后的整体刚度矩阵和整体荷载列阵。
此时，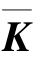
为正定阵，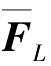
全部为已知量。
解方程组（2.62），可以得到整体结构位移结点δ，进而通过式（2.14）和式（2.23），可分别求出各单元的位移和应力，从而对结构进行变形与受力分析。