8.1 壳体的内力
薄壳理论是建立在和薄板理论相类似的两个基本假定上，通常也称为Kirohhoff假定，即：
①变形前垂直于中面的直线在变形后仍然是直线，与变形后的中面保持垂直，且长度不变（也称为直法线假定）。
②垂直于中面方向的应力与其他应力相比较，可忽略不计。
第一个假定忽略壳体的横向剪切变形和横向挤压变形；第二个假定忽略壳体的横向挤压应力。这样，就可以把壳体看作是由许多平行于中面的薄层所组成，它们互不挤压，单独的变形而又保持直法线的特性。于是，薄壳的变形问题就可以化为研究其中面的变形问题，这样三维问题就被简化为二维问题处理。
虽然基本假设相同，但薄壳和薄板之间还存在本质差别，即使在小挠度前提之下也是如此。在薄壳中，面内力（常称为薄膜内力）和弯曲应力同时存在并且相互影响，这会导致壳体的微分方程变得复杂，不能像面内变形的薄板那样进行简单的叠加。
由于壳体曲率的存在，因此可以面内力来平衡垂直于中面的外荷载，这在薄板小挠度情况下是不可能的。以面内力来平衡外荷载，这是壳体的特点和优点。面内力引起的应力沿厚度方向是线性分布的，在工程设计中，总是力图由面内力来平衡外荷载，避免弯曲内力出现。壳体内没有弯曲内力出现的状态称为“无矩状态”或“薄膜状态”，研究壳体无矩状态的理论称为无矩理论或薄膜理论。在无矩理论中，壳体可以有弯曲变形，但不产生内力矩和横向剪力。有变形而无相应的内力，这在刚度为零的情况下是可以的。
考察一壳体的微元体，如图8.1所示，Oabc是它的中面，Oxyz为建立在中面上的右手坐标系，z轴为中面法线，x，y轴与中面相切。与平板微元体不同，壳体的微元体是曲状的，中间在x向和y向的曲率半径为rx，ry。
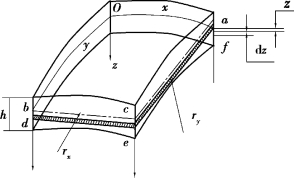
图8.1 壳微元体
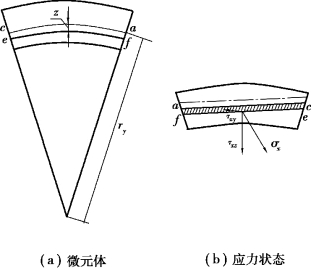
图8.2 壳微元体上的内力
现在，考察微元体截面上的内力，先看ac截面，在图8.2（a）中，为清晰起见，把ac截面的形状画得不是协调的。在z方向，截面有厚度h，而在宽度方向（ac方向或y方向）截面只具有微元体的长度，因此ac截面的形状应是厚度大大超过宽度。作用在ac截面上的应力，沿着y方向可以看成是不变的，而仅仅沿着z方向变化。由此，将ac截面看成是由一些平行于ac的“窄条”组成，图中示出典型的窄条ef，它与中面ac中距离为z，厚度为dz。ac截面并不是一个矩形，而为圆环的一部分。由关系式
得到
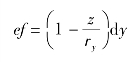
于是，ef窄条的面积为
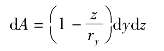
作用在窄条上的应力如图8.2（b）所示。所有如ef这样窄条上的应力就组成了ac截面的内力和内力矩，和在平板时的情形相似。去掉因子dy，得到的是单位长度上的内力和内力矩，它们分别是
x方向的拉力
顺剪力（中面内的剪力）
横剪力（与中面垂直）
弯矩
扭矩
再考虑bc截面，可类似得到如下的内力：
x方向的拉力
顺剪力（中面内的剪力）
横剪力（与中面垂直）
弯矩
扭矩
这些内力表达式的确立，已经规定了所有内力和内力矩的正向，如图8.3所示。为便于记忆，可做如下的理解：
①FNx，FNy以拉为正、压为负；
②Fxy，Fyx以与x，y轴正方向的夹角减小为正，反之为负；当Fx，Fy作用在法向与x，y轴正方向相一致的截面上时，与z轴的正方向一致为正；Mx，My以使z=
的曲面产生拉应力时为正；Mxy使O点及其对角c点翘向z轴的负方向为正。
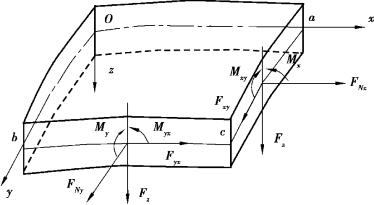
图8.3 薄壳内力
这就是说，上式的成立并不是剪力互等定律的直接推论，而是在计算内力值时近似地将截面形状看作矩形的缘故。
综上所述，壳体在每一点处有8个内力分量。在壳体的计算中，常先求内力，再按梁理论计算内力，即
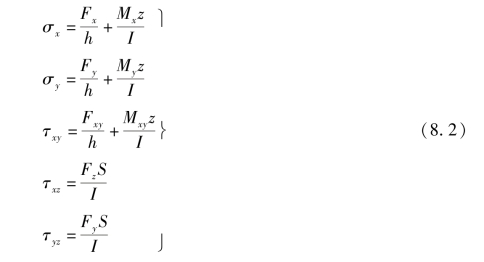
式中
内力FNx，FNy，Fxy引起的应力沿厚度均匀分布。弯矩Mx，My，Mxy引起的应力沿厚度线性分布，在中面为零，在两表面达到最大正、负值。横剪力Fx，Fy引起的剪应力沿厚度为抛物线分布，在中面为最大，在两表面为零。
内力FNx，FNy，Fxy常称为薄膜内力，它们的方向平行于中面，这是中面的拉伸、压缩、剪切而产生的。
弯矩Mx，My，横剪力Fx，Fy和扭矩Mxy常称为弯曲内力，它们是中面的弯扭变形而产生的。