▶2.4.2 应注意的几个问题
为了提高有限元计算的效率,以下几方面应受到重视。
(1)计算方案
对于所计算的工程问题,虽然在理论上任何物体都可看作三维体,但对实际分析来说,许多情况下应尽量根据分析目的简化问题。因此,在进行有限元分析时,首先应综合分析目的和研究对象的特点,确定所研究问题所属的类型,如平面问题、空间问题、轴对称问题或杆系问题等。这种确定是基于求解该具体问题的弹性数学模型所使用的理论假设。通常,结构分析中所遇到的问题可以归纳为如下几类:
①杆/桁架。
②梁。
③平面应力。
④平面应变。
⑤轴对称。
⑥板弯曲。
⑦薄壳。
⑧厚壳。
⑨一般三维体。
如分析不当就可能把复杂的问题过于简化,使许多应当考虑的因素没有考虑到;或者把简单的问题处理得过于复杂,没有略去本该简化的次要因素。
若计算方案不当,将直接影响计算工作量和计算精度,属于首要问题。
(2)单元选择
计算方案确定以后就可以确定选用哪一类单元,例如在结构分析领域中,常见的单元包含杆单元、梁单元、平面单元、板壳单元、实体单元以及其他特定单元等。在同一类单元内,还存在着选用哪种形式的单元的问题。例如,在平面应力问题中,选用三角形单元、矩形单元还是相应的曲边形单元等。甚至同一问题,根据分析目的的不同,可能采用在结构分析、构件分析和结点分析中,选用不同类型、不同阶次的单元。
对于同一问题,究竟选用什么单元最好(精度高、收敛快、计算量少),并没有一个成熟的方法,只能根据计算者对单元性质的理解和计算经验,针对具体问题予以选用,有时尚需进行试算。
(3)结点的选择及单元的划分
结点的布置与单元的划分相互关联。通常,集中荷载的作用点、分布荷载强度的突变点、分布荷载与自由边界的分界点、支承点等都应该作为结点。并且,当物体是由不同的材料组成时,厚度不同或材料不同的部分,也宜划分为不同的单元。
结点的多少及其分布的疏密程度,一般要根据所要求的计算精度、应力梯度、质量分布等来综合考虑。从计算结果的精度上讲,单元越小越好,但计算所需要的时间也会大大增加。往往计算机的硬件对计算规模也有限制。因此,在保证计算精度的前提下,应尽可能采用较少的单元。为了减少单元,在进行静力分析时,划分单元应考虑应力梯度较大的部位单元可以划分得细一些,而在应力变化比较平缓的区域可以划分得粗一些。
控制单元的规则性,避免过多的畸形单元,对计算误差也有重要意义。
(4)结点编号
结点编号,应尽量使同一单元的相邻结点的号码差尽可能地小,以便最大限度地缩小刚度矩阵的带宽,节省存储、提高计算效率。如前所述,平面问题的半带宽为
![]()
若采取带宽压缩存储,则整体刚度矩阵的存储量N最多为(https://www.daowen.com)
![]()
式中 d——相邻结点的最大插值;
n——结点总数。
如图2.16所示,图(a)与图(b)的单元划分相同,且结点总数都等于14,但两者的结点编号方式不同。图(a)是按长边编号,d=7,N=488;而图(b)是按短边进行编号,d=2,N=168。图(b)的编号方式可比图(a)的编号方式节省280个存储单元。
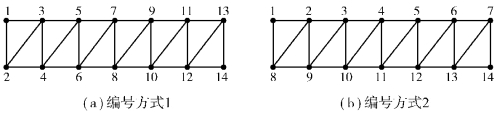
图2.16 结点编码方式的比较
(5)单元结点i,j,m的次序
在三角形单元中,为了在计算中保证单元的面积A不会出现负值,结点i,j,m的编号次序必须是逆时针方向。实际上,结点i,j,m的编号是可以任意安排的,只要在计算刚度矩阵的各元素时,对A取绝对值,即可得到正确的计算结果。在实际计算时,应该注意所选用的有限元分析软件的使用要求。
(6)应力计算结果的整理
静态有限元分析的计算结果主要包括位移和应力两方面。这里着重讨论对应力计算结果的整理。
由于三角形常应变单元是常应变单元,有限元分析软件计算出的应力,通常都是作为单元形心处的应力。为了能从计算结果推算出弹性体内某一点处接近实际的应力值,一般可采用绕结点平均法或两单元平均法进行处理。
所谓的绕结点平均法,就是将环绕某一结点的各单元常应力加以平均,用以表示该结点的应力。以图2.17中结点1和结点2为例,有
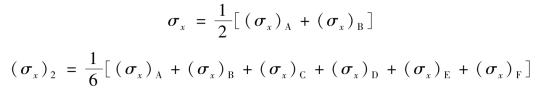
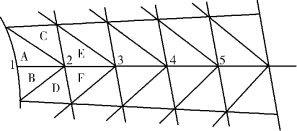
图2.17 绕结点平均法
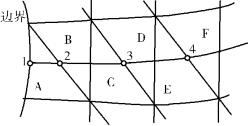
图2.18 两单元平均法
值得注意的是,为了使计算的应力能较好地表示结点的实际应力,环绕该结点的各个单元的面积不应相差太大。一般而言,绕结点平均法计算出来的结点应力,在内结点处较好,而在边界结点处则可能很差。因此,边界结点处的应力不宜直接由单元应力平均来获得,而应该由内结点的应力进行推算。例如,图2.18中的边界点1,做如下计算会更好一些:先用绕结点平均法算出内结点2,3,4处的应力,然后再用抛物线插值公式进行推算,即
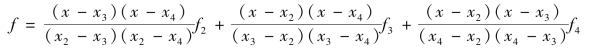
式中 x2,x3,x4——3个插值点2,3,4的坐标;
f2,f3,f4——相应的应力值。
只要将结点1的坐标x1代入式中便可求得近似的应力值。
另一种推算结点应力值的方法是所谓的两单元平均法,即把两个相邻单元中的常应力加以平均,用来表示公共边界中点处的应力。同样,为了使这样的计算应力具有较好的表征性,两相邻单元的面积也不应相差太大。对图2.18所示的情况,可取
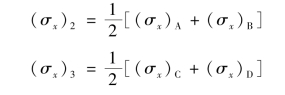
如果结点1位于内结点2,3,4的光滑连线上,则该点的应力也可由前述的抛物线应力插值公式进行推算。
