3.1　单元位移模式多项式选择

3.1　单元位移模式多项式选择

有限元位移解法中选择的单元位移模式是一种假设的试函数，用以近似地表示单元的位移场。因此，单元的精度主要取决于描述单元变形的位移模式的精度。

在位移解法中，位移函数大多采用多项式函数，这是因其具有便于计算、易于满足收敛性等特点。

为了保证随着单元逐渐加密时，位移、应变、应力能收敛于真实解，要求所选择位移多项式函数满足收敛性准则。由第2.2.7节讨论可知，完全一次多项式是保证完备性的必要条件。

选择单元位移函数的主要原则可概括为以下几方面：

①多项式项数决定了待定参数个数，其选择首先要考虑单元的自由度（或单元结点个数）。一般来说，待定参数个数需与单元结点自由度数相等，这是因为位移函数最终就是由等同个数的结点位移参数插值获得的。

②其次要考虑所研究问题的几何各向同性性质。因为位移模式应与局部坐标系无关，所以在构造的多项式位移模式中各坐标地位均等，不应有所偏惠，即坐标的对称。

③选择多项式的幂次应由低阶到高阶进行，尽量选取完全多项式（此时完备性得到满足）。研究表明，单元的精度由完全多项式阶次决定。一般来说，完全多项式阶次越高，单元的精度则越高。

④选择多项式项还应充分考虑相邻单元之间的协调性要求。

基于上述原则，在选择多项式时，可参照图3.1所示的Pascal三角形进行。

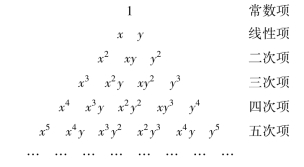
图3.1　Pascal三角形