▶6.3.3　单元刚度矩阵

▶6.3.3　单元刚度矩阵

单元刚度矩阵可由虚位移原理导出。假定单元的虚位移函数与单元位移函数的形式相同，即参照式（6.50）、式（6.55），则单元虚位移（δe）*和单元虚应变ε*可以写为

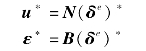
式中，N为形函数矩阵，（δe）*为单元的结点虚位移列阵，即

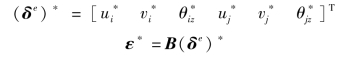
单元应力在虚应变上所做的虚功为

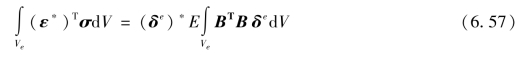
式中　Ve——单元体积。

将单元结点力记为

式中　FN——单元的轴力；

　　　FS——y方向的剪力；

　　　M——绕Z轴的弯矩。

单元结点力在虚位移上所做的虚功为

由虚位移原理，可得

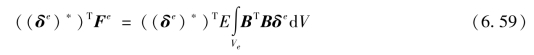
因为虚位移是任意的，所以为使式（6.59）成立，等式两边与（（δe）*）T相乘的项应该相等，即

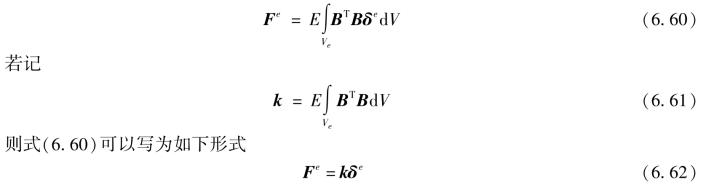
这就是表示梁单元的结点力与结点位移关系的单元刚度方程，而k即为单元刚度矩阵。将式（6.54）代入式（6.61），并经过积分运算，可以得到梁单元刚度矩阵的如下显式表达式

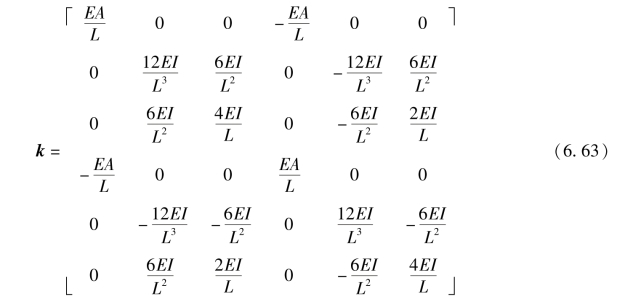
式中　A——单元的横截面面积；

　　　I——横截面惯性矩；

　　　E——材料的弹性模量。