▶3.3.2 8结点矩形单元(二次单元)
2026年01月14日
▶3.3.2 8结点矩形单元(二次单元)
图3.9为8结点矩形单元,在4个角点和各边中点设置结点,单元有16个自由度。单元结点位移列阵和单元结点力列阵分别为
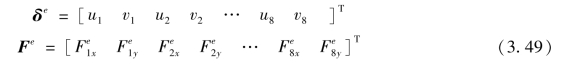
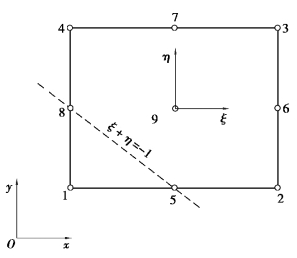
图3.9 8结点矩形单元
(1)单元位移模式
参照Pascal三角形,首先选择完全二次项:1,x,y,x2,xy,y2,有6个待定参数。其次,应在3次及以上项中选择2项。单元在边界上各包含3个结点,考虑到收敛性以及坐标对称性,位移函数在边界上x或y的最高幂次应为2次,故选择x2y,y2x两项。显然,如此选择位移模式能够满足连续性要求。
单元位移模式取如下形式
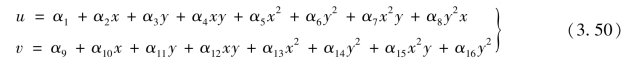 (https://www.daowen.com)
(https://www.daowen.com)
式(3.50)为不完全3次多项式,单元位移模式包含完全的一次项,满足完备性要求。由于矩形单元其边界总是平行于坐标方向的,因此,在任意边界上位移函数均为x或y的二次函数。单元各边界均包含3个结点,可唯一确定二次函数,能够保持相邻单元公共边界上位移的协调性,因此该单元为完备协调元。
(2)构造形函数
单元位移插值函数为

构造主结点形状函数N1,设
![]()

单元刚度矩阵和单元等效荷载的计算可参照式(3.47)和式(3.48)。
