1.3　有限单元法基本概念

从选择基本未知量的角度可分为3类：位移法、力法和混合法，其中以位移法应用较为广泛。本书着重介绍基于弹性理论的以位移为未知量的有限单元法的基本理论，及其在结构分析中的初步应用。

这里先介绍经典的变分问题近似解法——里兹法。里兹法是先假设未知解为带有未知参数的已知函数（试函数）。代入泛函表达式后得到由未知参数来表示的泛函。应用变分原理，根据泛函的极值条件，得到n个线性代数方程。解出未知参数，也就得到了问题的近似解答。这种方法可以说是通过对函数的“离散”而得到方程组的。它的困难在于所试选函数必须满足整个区域的边界条件，这在一般情况下是十分困难的，有时甚至是难以做到的。

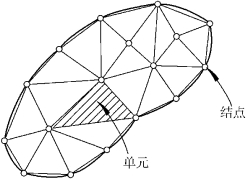
图1.2　连续介质的离散过程

有限单元法的基本思想，就是对求解的弹性域进行离散化，即将具有无限多个自由度的连续体，化为有限多个自由度的结构体系。具体来说，就是将具有无限自由度的整个弹性域用有限多个、有限大小（微小）且相互之间仅在有限多个点处连接的一系列区域的集合体来替代（图1.2）。这些微小的区域称作单元，各单元间相互连接点称作结点。整体结构将以结点位移参数作为基本未知量（有限自由度）。这一区域剖分的过程称作结构离散化过程，即建立有限元数值分析模型。

其次是考虑单元的平衡。在单元区域内设置一个函数表示任意点位移随位置变化形态，这种假设的试函数称为位移模式，在一般情况下，它应当满足单元之间位移的连续性。按照函数插值理论，将单元内任意点的位移通过一定的函数关系用结点位移参数来表示，即位移插值函数。随后则从分析单元入手，采用能量原理建立单元基本方程。这一过程称作单元分析。

再把所有单元集合起来，进行整体受力分析，得到一组以结点位移参数为基本未知量（自由度）的多元代数方程组，称为结构或求解区域的有限单元法整体分析方程。结合位移边界条件即可求解结点位移参数。这一过程称为整体分析。

解出结点位移参数后，可根据单元位移插值函数以及弹性理论基本方程得出弹性域任意点的应变和应力。

将整个弹性域剖分和以有限的结点位移参数为基本未知量是有限单元法的基本构想和分析问题的出发点。

对于实际工程结构的多样性、荷载与边界约束的复杂性，有限单元法解的基本思想就是采用基于能量原理的变分方法将难以求解的弹性理论基本方程中多元偏微分方程组变换为求解多元代数方程组，使得结构分析易于实现。