▶6.4.1　平面梁单元

▶6.4.1　平面梁单元

如图6.5所示为一个具有2个结点的平面梁单元，取两个直角坐标系，总体坐标系为Oxy，局部坐标系为O＇x＇y＇，两个坐标系间的夹角为α，梁单元的轴线与局部坐标系的x＇轴重合。

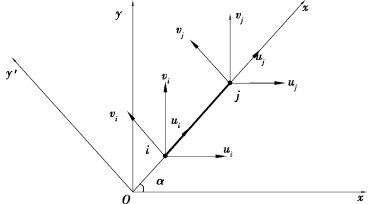
图6.5　平面梁单元

令梁单元在局部坐标系下的结点位移和结点力分别为

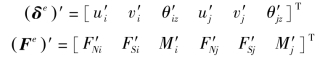
在总体坐标下的结点位移和结点力分别为

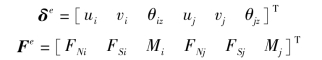
将6.3节建立的单元刚度矩阵与图6.5中的梁单元相对应，即把图6.4的坐标系看作图6.4中的局部坐标系。对于局部坐标系来说，单元刚度矩阵元素表示的局部结点位移u＇，v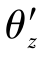＇，与局部坐标系中的结点力的关系，见式（6.62）

局部坐标系下的结点位移与总体坐标系下的结点位移有如下关系

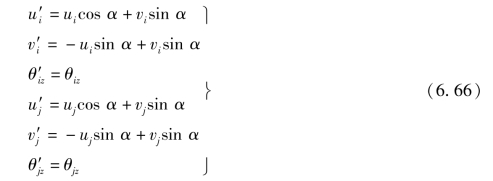
将式（6.66）写成矩阵形式，则有

式中　T——梁单元的坐标转换矩阵。

对于局部坐标系下的结点力（Fe）＇和总体坐标系下的结点力Fe，同样有与式（6.69）类似的转换关系，即

式（6.74）即是总体坐标系下，表示梁单元的结点力和结点位移之间关系的单元刚度方程。

由上述推导过程和式（6.73）可知，对处于任意方位的平面梁单元的刚度矩阵，可以利用局部坐标系下的单元刚度矩阵k＇，通过坐标转换来得到。在有限元程序中，一般是先在单元局部坐标系下计算单元刚度矩阵，然后按式（6.73）将其转换为总体坐标系下的单元刚度矩阵，最后再将总体坐标系下的单元刚度矩阵组装到总体刚度矩阵中去。