▶4.1.3　10结点四面体单元（二次单元）

▶4.1.3　10结点四面体单元（二次单元）

图4.6所示为10结点四面体单元，单元结点位移列阵可表示为

式中

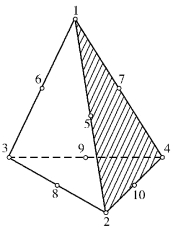
图4.6　10结点四面体单元

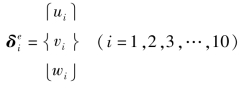
单元结点力列阵可表示为

式中

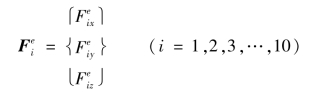
（1）单元位移模式

利用图4.4，单元位移模式可设置为完全二次多项式，即

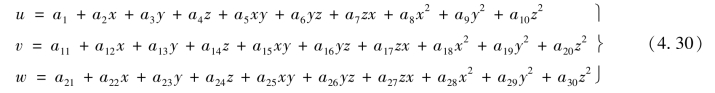
考察单元收敛性。

显然，位移函数满足完备性。对于单元的边界面，例如124组成的面（图4.6），L3=0，由式（4.4）可得

从上式解出z，然后代入式（4.30），则位移函数可表示为

位移函数为完全二次式，可由该面6个结点1，2，4，5，7，9位移参数唯一确定，因而单元位移函数满足协调性。

（2）位移插值函数

单元插值函数可以表示为：

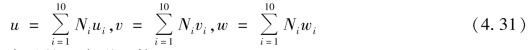
式中　Ni——用体积坐标表示的二次形函数。

采用划面法直接构造单元形函数。

根据形函数性质（1），对于角结点1，设

其中包含了通过结点5，6，7的平面方程2L1-1=0与通过结点2，3，4的平面方程L1=0，故

由（L1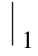）=1，得到c=1，因此

同理，可得N2，N3，N4。

对于边结点5，设

上式包含了通过结点1，3，4的平面方程L2=0与通过结点2，3，4的平面方程L1=0，由，得到c=4，因此有

同理，可得N6～N10。

于是，10结点四面体的形函数可表示为

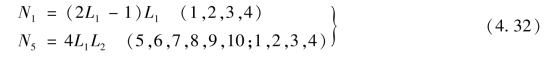
（3）单元刚度矩阵和单元等效荷载

空间问题单元刚度矩阵一般可表示为

式中　B——几何矩阵，可写成分块形式

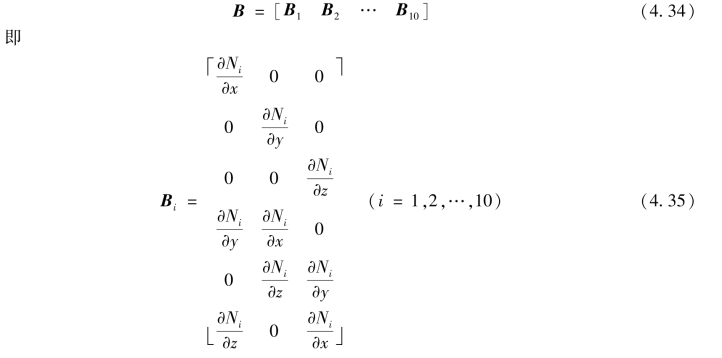
其中，由式（4.10）求得

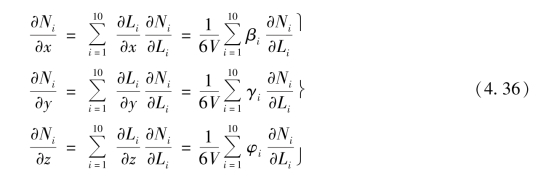
k可按结点分块写成

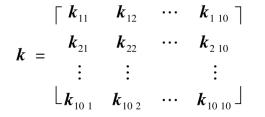
则子矩阵krs为

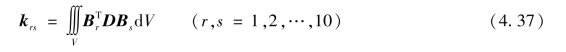
单元等效荷载为列阵

式中

单元等效荷载计算可参照式（4.27）计算。