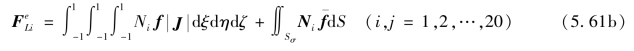5.5 20结点六面体三维等参单元
对于三维结构的有限元分析，高阶单元往往更具有计算效率。二次等参元既能适应复杂结构的曲面边界，又便于构造高阶单元，在三维应力分析中较为常用。目前在三维问题的等参元应用中，较为常用的是20结点六面体等参元，已被采用于多种通用有限元分析程序，在复杂的三维结构分析中取得了相当的成功。
图5.10（b）为一个任意20结点曲面六面体单元，取8个角点，12条棱边的中点为结点。建立一个与此单元对应的边长为2的20结点正立方体单元，并建立局部坐标系ξηξ，坐标原点在正立方体的形心，如图5.10（a）所示。此规则单元为任意20结点六面体曲面元的母单元。
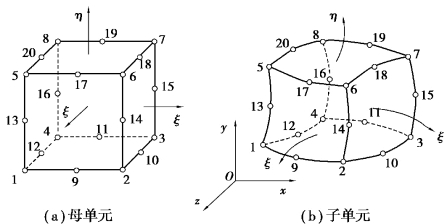
图5.10 20结点的六面体等参元
（1）母单元位移函数
参照式（4.56），母单元的位移模式设为
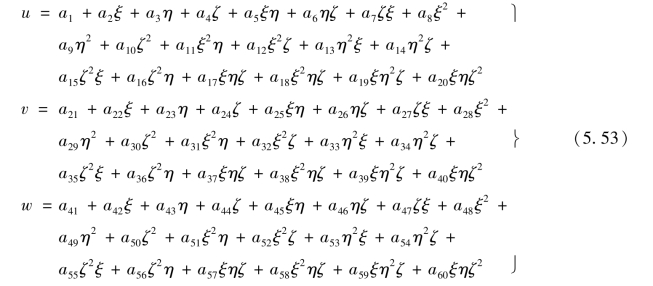
单元结点位移列阵和单元结点力列阵分别为
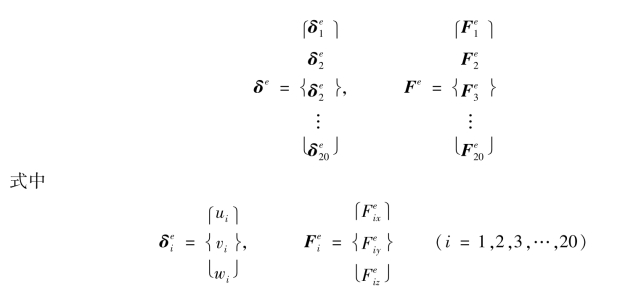
单元位移插值函数可以表示为
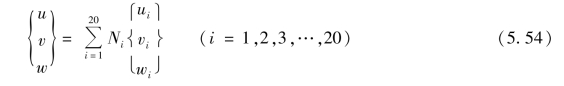
式中，Ni（ξ，η）为形函数，参照式（4.59）由式（5.55）给出
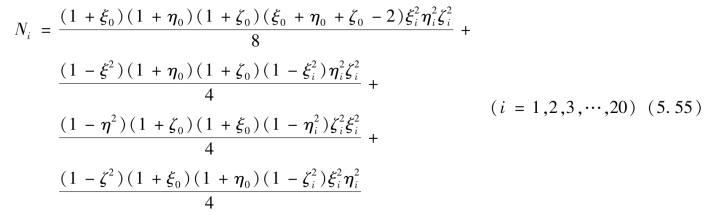
其中ξ0=ξξi，η0=ηηi，ζ0=ζζi。
（2）等参坐标变换
对图5.10（b）所示整体坐标系xyz与图5.10（a）所示局部坐标系ξηζ两种坐标系采用式（5.56）进行变换
式中，变换函数Ni（ξ，η）即为位移插值函数（5.54）中的形函数。
坐标变换式（5.55）使实际的六面体曲面子单元与正立面体母单元的8个角结点、12个边结点一一对应，子单元6个曲面、12条曲边与母单元6个平面、12条直边一一对应，并使子单元内各点与母单元相应各点一一对应。这样相当于把实际的任意曲面六面体子单元映射为正立方体母单元。
（3）单元刚度矩阵
三维变形状态下，一点的应变与位移的几何关系，写成矩阵形式为
式中，B为几何矩阵，可按结点分块表示为
式中
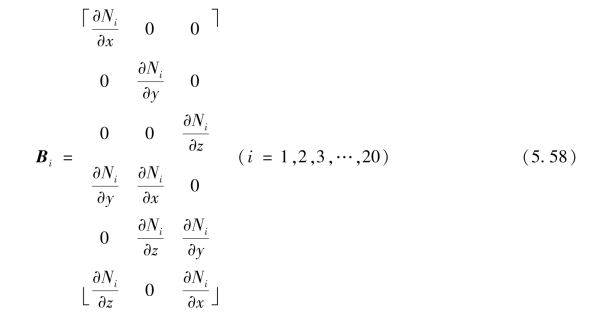
由最小势能原理，可得单元刚度矩阵为
按照前述分析，单元刚度矩阵可写为
式中 J——坐标变换的雅可比矩阵行列式。
k可按结点分块写成
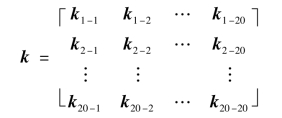
则子矩阵ki-j为
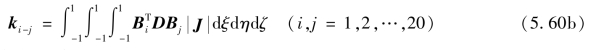
（4）单元等效荷载列阵
设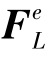
为单元等效荷载列阵
式中
单元等效荷载列阵按式（5.61a）
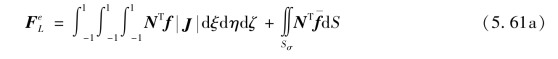
单元等效荷载列阵子块
