8.3 曲面薄壳单元
在上面几节,用折板结构代替实际壳体,只要计算网格比较密集,计算精度是可以满足工程要求的。但如果直接采用曲面单元,因其能够反映壳体的真实几何形状,可以得到更好的计算结果。
如图8.9所示,在壳体中面上布置s个结点,中面上任一点的坐标可表示如下:
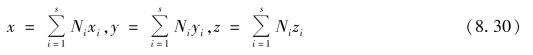
式中 Ni——二维形函数。
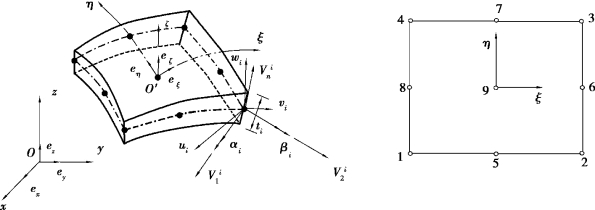
图8.9 9结点曲面壳单元
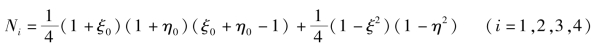
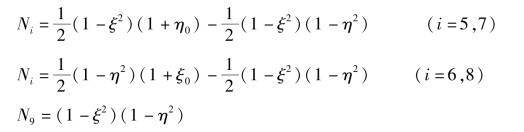
变形前,单元内任一点的坐标为

假定变形前的中面法线在变形后仍为一直线(但不一定继续垂直于中面),沿此直线的单位矢量为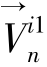 ,则变形后任一点的坐标为
,则变形后任一点的坐标为
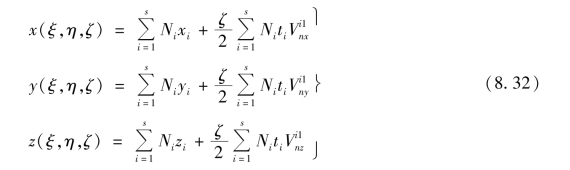
由式(8.32)减去式(8.31),得到单元内任一点的位移分量如下:
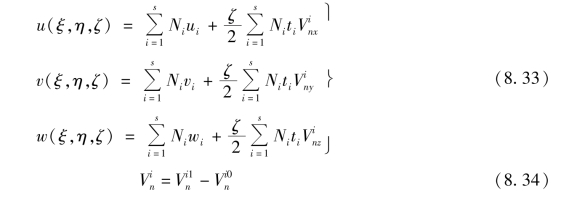
![]() 的3个分量,实际上是中面法线方向余弦的增量。它们可用结点i的转动表示,但没有唯一的表示方法。一个比较有效的方法是定义正交于
的3个分量,实际上是中面法线方向余弦的增量。它们可用结点i的转动表示,但没有唯一的表示方法。一个比较有效的方法是定义正交于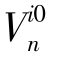 的两个矢量
的两个矢量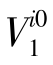 和
和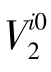 。首先,让
。首先,让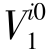 为同时正交于y轴和
为同时正交于y轴和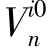 的单位矢量,即
的单位矢量,即

其中(u,v,w;x,y,z)表示将u依次换成v,w,并把x依次换成y,z,就可得到v,w的偏导数∂v/∂ξ,∂v/∂η,∂v/∂ζ和∂w/∂ξ,∂w/∂η,∂w/∂ζ。
为了得到位移对x,y,z的偏导数,可利用如下关系:
 (https://www.daowen.com)
(https://www.daowen.com)
式中 J——雅可比矩阵。
将式(8.39)代入式(8.41),得到
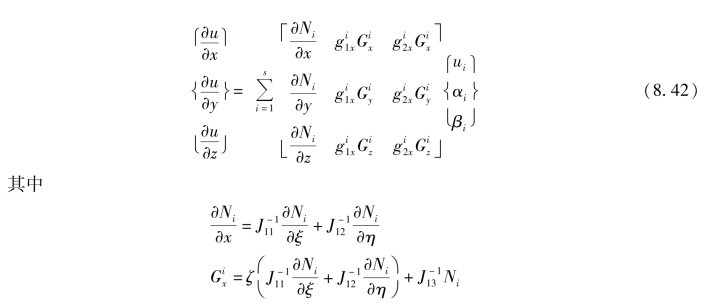
其中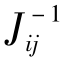 是J-1的(i,j)元素。同样,可求出v,w的偏导。
是J-1的(i,j)元素。同样,可求出v,w的偏导。
由此得到
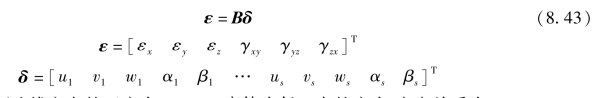
假定壳体中面法线方向的正应力σζ=0,壳体内任一点的应力-应变关系为
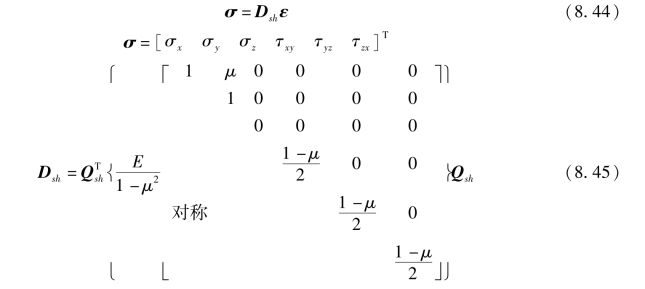
矩阵Qsh把应力-应变关系从局部坐标系(ξ,η,ζ)变换到整体坐标系(x,y,z)。Qsh的元素可用ξ,η,ζ在(x,y,z)坐标系的方向余弦表示如下:
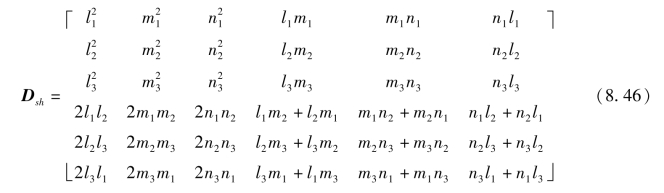
其中
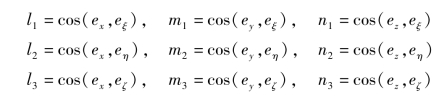
单元刚度矩阵计算如下:
![]()
在一般情况下,计算壳体单元刚度矩阵时沿3个方向进行数值积分,并且在每个积分点都要重新计算Qsh和Dsh。但在某些特殊情况下,同一类型的单元具有相同的Dsh,只要计算一次,然后重复利用。
本壳体单元具有下列优点:
①可准确地代表各种复杂的壳体外形。
②完全满足了变形连续条件。
经验表明,采用9结点壳体单元,计算精度是不错的。
