5.2 4结点四边形平面等参单元
本节以平面4结点平面等参单元为例，介绍等参单元的坐标变换、单元位移函数的构造、单元刚度矩阵和等效结点荷载的计算等。
图5.3（b）为整体坐标x，y中的任意4结点四边形单元，建立一个与此单元对应的边长为2的4结点正方形单元，并在其形心位置建立局部坐标系ξ，η，如图5.3（a）所示。
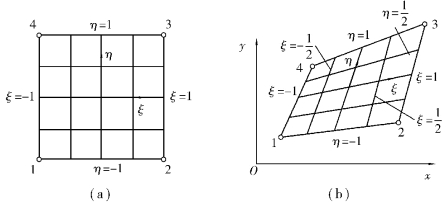
图5.3 4结点平面四边形单元
（1）局部坐标系的单元位移函数
参照式（3.50），在局部坐标系中，单元位移模式可取为
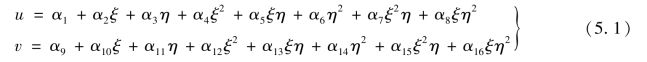
单元位移插值函数为
式中，Ni（ξ，η）为形函数，参照式（3.46）可取为
式中，ξ0=ξiξ，η0=ηiη。
式（5.2）用矩阵表示为
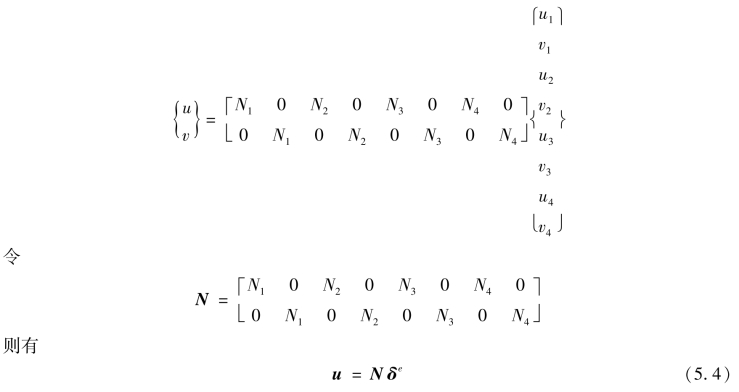
（2）等参坐标变换
如图5.3（b）所示为整体坐标系的任意四边形单元，同样设置4个结点，对两种坐标系采用式（5.5）进行变换：
式中 Ni（ξ，η）——位移插值函数中的形函数，由（5.3）表示。
由式（5.5）可以看出，通过坐标变换图5.3（b）整体坐标x，y中的任意四边形单元映射为图5.3（a）局部坐标ξ，η中的正方形单元。任意四边形的4个角点1，2，3，4与正方形的4个角点1，2，3，4一一对应，任意四边形的4条边界与正方形的4条边界一一对应，正方形中任意点（ξ，η）与曲边四边形中相应的点（x，y）一一对应。上述正方形单元称作母单元，任意四边形单元称作子单元。
例如，对于ξ=1的边界（通过结点2和3的边界），将式（5.3）代入式（5.5），得
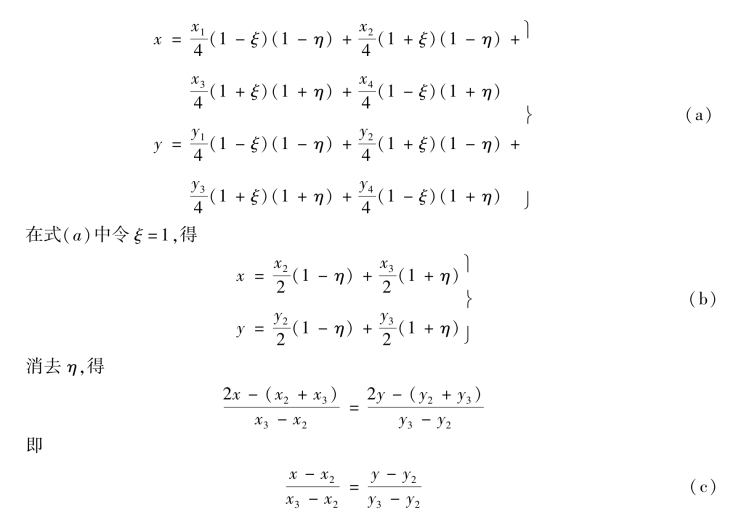
式（c）即为xy平面内通过结点2，3的直线方程。同理，可以推得任意四边形子单元其他3条边与母单元中ξ=-1，η=±1边一一对应，且子单元形心与母单元形心对应。
采用坐标变换式（5.4）后，xy平面内任意的四边形单元都可以映射成ξη平面上的正方形母单元。且直线仍映射为直线，仅其长度和位置发生了转化，故称该种变换为线性变换，子单元为线性等参元。
（3）单元刚度矩阵
将式（5.2）代入平面问题的几何方程，得到单元的应变
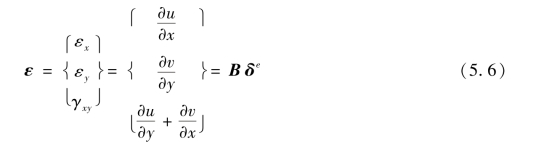
式中，B为几何矩阵
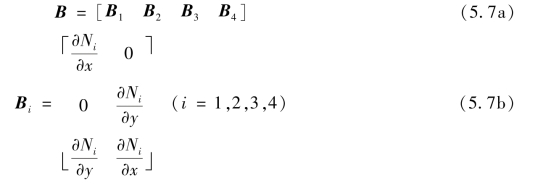
由于形函数Ni为局部坐标（ξη）的函数，所以根据复合函数求导法则可得
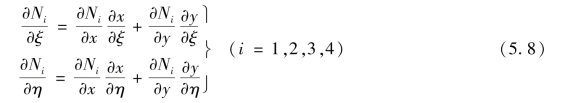
或用矩阵表示为
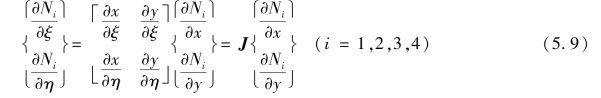
式中，J为雅克比矩阵
其元素可以利用坐标变换式（5.5）计算得到，即
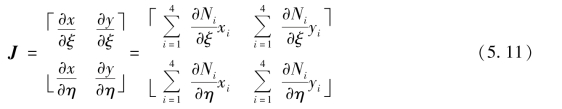
将式（5.9）两边左乘以雅可比矩阵的逆矩阵J-1可以得到
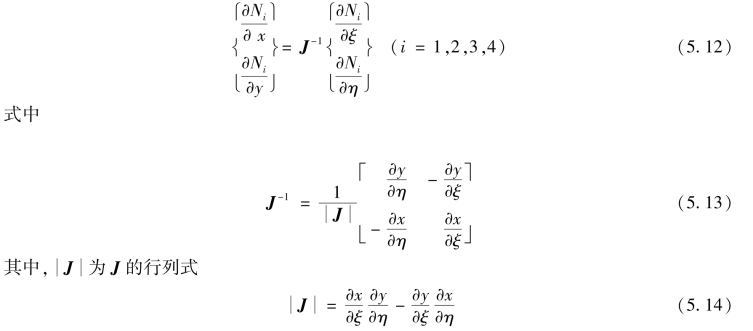
将式（5.5）代入平面问题的物理方程，得到单元的应力
式中 S——单元应力矩阵。
参照式（2.32），根据最小势能原理，单元刚度矩阵可表示为
式（5.16）中，被积函数是局部坐标ξ和η的函数，应对积分元进行变换。
设i，j分别为整体坐标x，y方向的单位向量，dξ，dη分别为局部坐标ξ，η在整体坐标系下的微元向量，可表示为
在整体坐标系中，由dξ及dη所组成的微元面积为
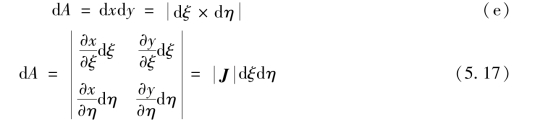
故式（5.16）可以写为如下形式
式（5.18）的被积函数是局部坐标（ξη）的函数，难以得到显式表达。所以，等参单元刚度矩阵的积分计算一般采用数值积分计算。
（4）单元等效结点载荷
设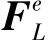
为单元等效荷载列阵，其子块为
式中
参照式（2.45），由虚功原理可得
式中 f——单元体力；
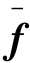——单元面力。
由于
，故
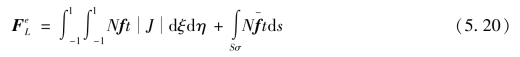
对于式（5.20）中面积微元ds，例如在ξ=c（常数）的曲线上，dη在整体坐标内的线段微元的长度为
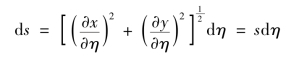
其他边界上的ds可以通过轮换ξ，η得到。
当所给表面力沿曲边的法向和切向时，即f-=[στ]T时，可将式（5.20）中的第一类曲线积分化为第二类曲线积分形式
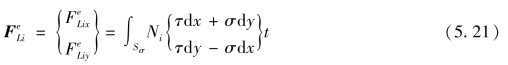
其中规定σ沿外法向为正，τ以沿单元边界前进使单元保持在左侧为正。
式（5.20）一般采用高斯积分法计算。
下面分析如图5.4所示的表面力计算方法。
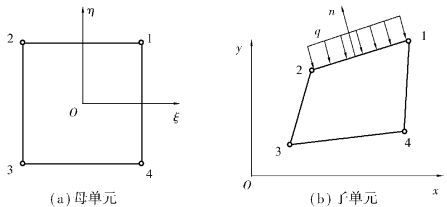
图5.4 4结点四边形等参元表面力计算
由于表面力q所在的边对应于η=1的边界，设n为该边界外法线n在整体坐标系的方向向量
为外法线表面力在整体坐标系的向量，则
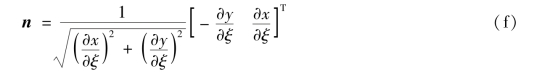
因为规定压力为正，拉力为负，则当表面力为压力时，压力方向与外法线方向相反，因此，表面力可以表示为
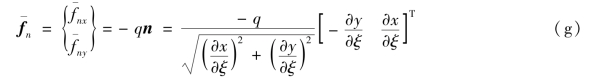
而式（5.20）微元为
将式（g）、式（h）带入式（5.20），则可得到单元表面力的等效结点荷载
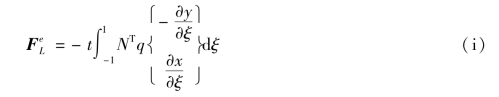
因为假定作用的表面力所在的边对应于η=1的边，所以积分只沿η=1的边（相当于实际单元的12边）。这时N3，N4等于零，且N1，N2中的η=1，计算结果为只在结点1，2上产生等效结点荷载。
当表面力作用在单元的其他边上时，同时可以得到相应的计算公式。
【例5.1】 计算图5.5所示单元的表面力的等效结点荷载（假定单元厚度为t）。
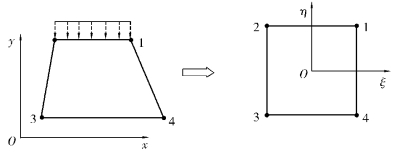
图5.5 等参元表面力等效荷载计算
【解】 对于图5.5所示情况，表面力的等效结点荷载可按式（5.21）计算。
因为积分只沿η=1的边进行，在该边上N3=N4=0，所以根据式（5.4），在边12上有
式中，l12是12边的长度。计算结果为将该边上的表面力平均分配到了该边的两个结点上。
结构整体方程的建立以及整体刚度矩阵K与整体结点荷载列阵FL集成，前面已经详细介绍，不再赘述。