▶3.2.2 6结点三角形单元（二次单元）
如图3.3所示为6结点三角形平面单元，除三角形角点以外，3条边的中点各设置一个结点。
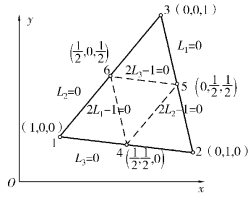
图3.3 6结点三角形平面单元
单元结点位移列阵为
式中
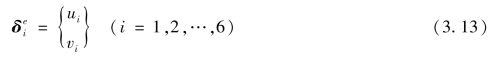
单元结点力列阵为
式中
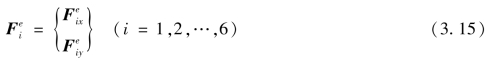
（1）单元位移模式及其收敛性
单元具有6个结点，12个自由度，参照图3.1所示Pascal三角形，单元位移模式设置为完全二次多项式，包含12个待定常数：
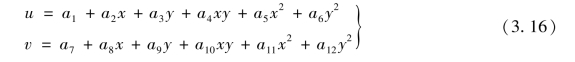
式（3.14）包含完全一次多项式，因此，单元的完备性得到满足，下面考察其连续性。
图3.4所示，两个相邻的6结点三角形单元，结点2，5，3连线为其公共边界。对于单元①，位移模式（3.16），使得单元位移函数在公共边界上为坐标的二次函数，且由结点2，5，3确定的二次函数是唯一的。同理单元②的位移函数在公共边界亦为由结点2，5，3唯一确定的二次函数，于是，在弹性体变形过程中相邻单元公共边界上位移始终保持协调，因此，由式（3.16）所确定位移函数的单元为完备协调单元。
（2）构造形函数
利用形函数的性质直接构造单元插值函数。
单元位移插值函数为
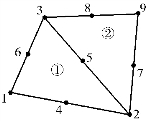
图3.4 相邻单元的连续性
分别考察N1和N4的构造。
根据形函数性质（1）（见2.2.3节），设
如图3.3所示，式中包含了通过结点4，6的直线方程
与通过结点2，5，3的直线方程L1=0，因而，
。由
，得到c=2。代入上式可得
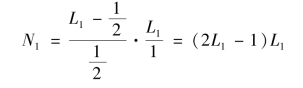
可以证明，式（3.18）满足根据形函数性质（2），即
为叙述方便，形象地将上述直接构造单元形函数的方法称为划线法。实际上，可以利用划线法可直接构造3结点三角形单元（一次单元）的形函数，即
结果与式（2.11）完全相同。
（3）单元刚度矩阵
单元基本方程应用最小势能原理建立，其过程与第2.2.6节讨论完全相同。由式（2.37）有
由于形函数Ni是面积坐标L1，L2，L3的函数，单元刚度矩阵k参照式（2.38）应写作
式（3.19）的计算参照面积坐标积分公式（3.10）。
（4）单元等效结点荷载
单元等效结点荷载可参照（2.45）写作
式（3.20）可按照面积坐标积分公式（3.10）和式（3.11）计算。
【例3.1】 均质平板，厚度为t，容重ρg，重力作用方向沿y轴负方向。试求6结点三角形单元的等效结点力。
【解】 将体力
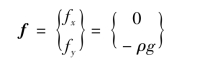
代入式（3.20）中体积力等效结点力公式，得：
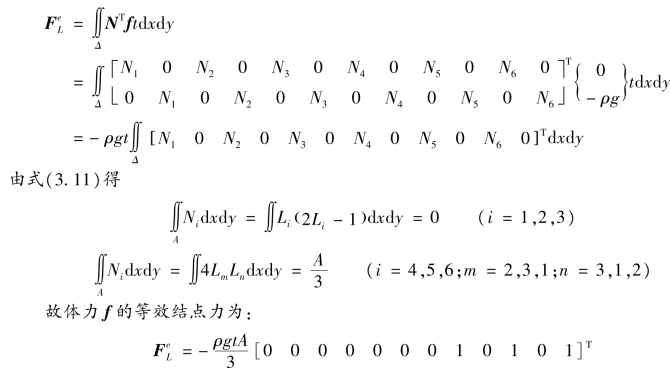
可以看出，6结点三角形单元承受自重荷载时，只需向3个边中结点各移置单元自重的
，3个角结点上等效结点力为零。该结果与静力等效结果有所不同。
整体结构分析的方法与过程在第2.3节已做详细介绍，这里不再赘述。