▶7.1.2　小挠度薄板弯曲问题基本方程

▶7.1.2　小挠度薄板弯曲问题基本方程

根据基本假定（1），有

于是由几何方程（1.6）第三式则有：=0，从而得到

这就是说，横向位移w只是x，y的函数，不随z而变。因此，在中面的任一根法线上的点都具有相同的横向位移，也就等于挠度。

根据式（7.1），几何方程（1.6）第五、六式得

从而得

此时，薄板小挠度弯曲问题中的几何方程和薄板平面应力问题中的几何方程是相同的，即

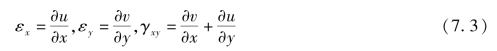
根据基本假定（2），有

也就是说，中面是中性层。

将式（b）对Z积分，并注意w只是x，y的函数，即得

将式（c）代入，得f1（x，y）=0，f2（x，y）=0。于是纵向位移表示为

于是，薄板位移函数可写作

可见，在薄板的小挠度弯曲理论中，只有w为独立的位移函数。

需要说明的是，在上述计算假定中虽然采用了εz=0，γzx=0，γyz=0，但在考虑平衡条件时，仍然必须计入3个次要的应力分量τxz，τyz和σz。事实上，在薄板的小挠度弯曲理论中，3个次要的应力分量τxz，τyz和σz可利用平衡方程由3个主要的应力分量σx，σy，τxy推导而得。

在薄板的小挠度弯曲理论中，放弃了关于εz，γzx和γyz的物理方程，即物理方程（1.14）中的第三、第五和第六式。根据基本假定（3），因为不计σx所引起的形变，所以薄板的物理方程为

可见，薄板小挠度弯曲问题中的物理方程和薄板平面应力问题中的物理方程也是相同的。

参照式（1.16），式（7.6）可写作

式中

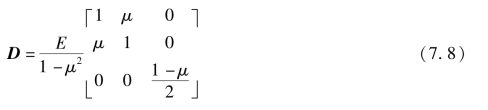
综上所述，薄板小挠度弯曲问题中，3组基本未知量分别为：应力分量σx，σy，τxy，应变分量εx，εy，γxy，以及位移分量板中面挠度w。