▶6.4.2 空间梁单元
(1)局部坐标系下的三维梁单元
如图6.6所示为一空间局部坐标系下的2结点空间梁单元,该单元和平面梁单元的区别在于,三维梁单元不但能够承受轴力、剪力和弯矩,还可以承受扭矩,而且可以在两个坐标面内同时承受弯矩。另外,三维梁单元的每个结点有6个自由度,也称为6个广义位移,它们是沿3个坐标轴方向的位移u',v',w'和绕3个坐标轴的转角![]() ,其中
,其中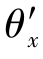 表示绕x'轴的转角,
表示绕x'轴的转角,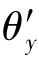 表示绕y'轴的转角,
表示绕y'轴的转角,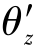 表示绕z'轴的转角。与6个广义位移对应,每个结点有6个广义力:
表示绕z'轴的转角。与6个广义位移对应,每个结点有6个广义力:![]() ,其中,
,其中,![]() 是沿梁轴线方向的轴力,
是沿梁轴线方向的轴力,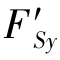 和
和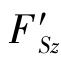 分别是沿y'轴方向和z'轴方向的剪力,
分别是沿y'轴方向和z'轴方向的剪力,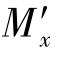 是绕x'轴的扭矩,
是绕x'轴的扭矩,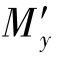 和
和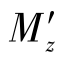 分别是绕y'轴和z'轴的弯矩。
分别是绕y'轴和z'轴的弯矩。
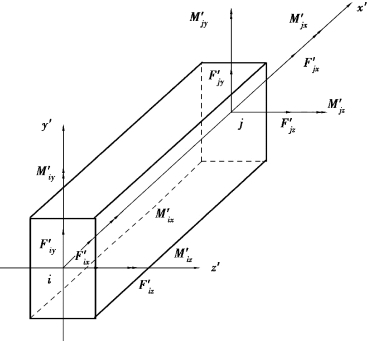
图6.6 局部坐标系下的三维梁单元
在x'y'平面内受力的梁单元的刚度矩阵式(6.63)、结点力和结点位移关系的刚度方程(6.62)已在第6.3节中给出,单元刚度方程(6.62)表示的是单元结点力![]() 和单元结点位移u',v',
和单元结点位移u',v',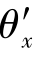 之间的关系,同时可以导出结点力
之间的关系,同时可以导出结点力![]() 的关系,然后将它们综合到一起,就可以得到局部坐标系内的空间梁单元的刚度矩阵,见式(6.77)。
的关系,然后将它们综合到一起,就可以得到局部坐标系内的空间梁单元的刚度矩阵,见式(6.77)。
对于局部坐标系下的三维梁单元,其结点力与结点位移的关系可以写成
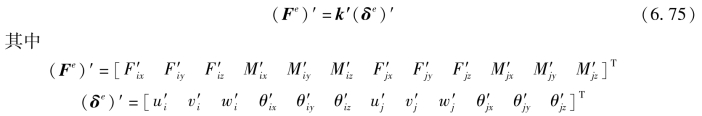 (https://www.daowen.com)
(https://www.daowen.com)
(2)总体坐标系下的三维梁单元
要进行三维刚架的有限元分析,需要将局部坐标系下建立的单元刚度矩阵转换到总体坐标系中,转换原理和方法与平面梁单元的坐标转换相同。
总体坐标系下的梁单元刚度矩阵k可通过如下转换得到
![]()
其中,k'是局部坐标系下的三维梁单元的刚度矩阵,见式(6.77),T是三维转换矩阵,转换矩阵可以根据单元的总体结点坐标求出,具体计算方法可参考有关文献。

在式(6.77)中,A为横截面面积,L是单元长度,Iy和Iz分别为横截面对y',z'轴的主惯性矩,Jk是扭转惯性矩,E和G是弹性模量和剪切模量。
