9.3 结构动力特性分析
动力特性分析的主要内容是求解固有频率和振型。对于自由振动，则结构动力方程（9.13）可简化式为
式（9.26）为二阶常系数线性齐次微分方程组，其解的形式为
代入式（9.26），得
齐次方程组（9.27）有非零解的条件为
式（9.28）即为式（9.26）的特征方程，是ω2的n次实系数方程，n为矩阵阶数。
在特征方程（9.28）中，刚度矩阵K是对称的，引入约束条件消除刚体位移后K是正定的。采用一致质量矩阵时M也是正定的，且有与K相同的带状性质；采用团聚质量矩阵且又考虑转动惯量或不考虑转角自由度时，M也是正定的。
求解方程（9.27）的问题称为广义特征值问题，式（9.27）的解ω2=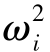
及其对应的矢量
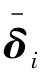（i=1，2，…，n ）分别称为特征值和特征向量。
利用刚度矩阵K的正定性质，可以将广义特征值问题方便地化为标准特征值问题。首先将K分解为
其中L为下三角阵。式（9.27）成为
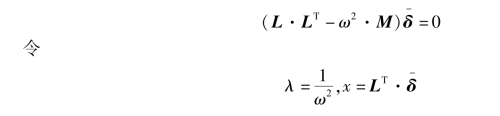
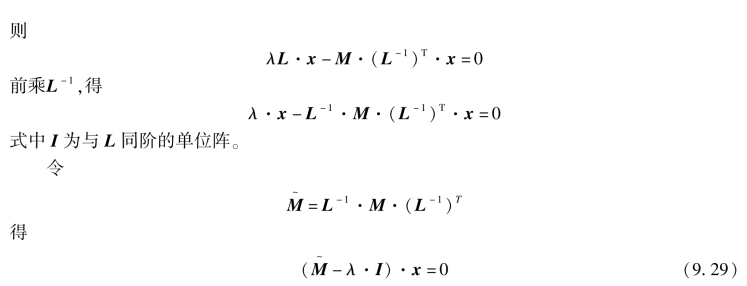
式（9.29）即为式（9.27）对应的标准特征值问题。
如果质量矩阵M是正定的，式（9.27）也可化为下述形式的特征值问题
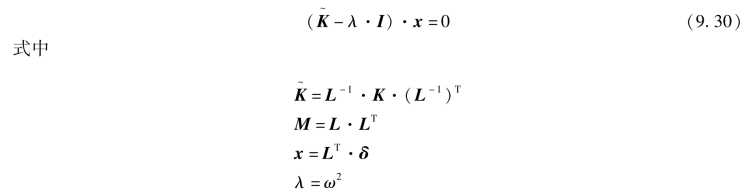
变换后的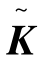
阵和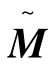
阵仍具有对称正定性质，但带状特性一般不再保留。
求解标准特征值问题式（9.29）或式（9.30），可以得出特征值ωi和与其对应的特征向量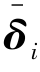
（i=1，2，…，n）。求解可采用广义雅克比方法。
结构振动分析问题与静力分析问题的根本区别是增加了与加速度有关的惯性力及阻尼相关的阻尼力项，作用力及结构响应都是随时间而变化的。动力分析的常见类型如下：
①模态分析。分析结构的振动参数，如固有频率及振型，以用于控制外加荷载频率或改变结构固有频率，以避免共振现象的出现。它也是模态叠加分析方法的基础。
②频率响应分析，又称为谐响应分析。分析结构在周期性荷载作用下的稳态响应。在周期性荷载作用下，结构响应的瞬态部分在阻尼的作用下很快就会消耗掉，最终只剩下稳态响应部分。频率响应分析可以使设计者避免共振、疲劳以及其他有害强迫振动作用的影响。
③瞬态响应分析，又称为时程响应分析。分析结构在随时间变化的荷载作用下的瞬态响应，得到随时间变化的位移、速度、加速度及应力。
④响应谱分析。利用“谱”计算结构响应的一种方法，主要用来替代时程响应分析，决定结构在随机荷载，如地震、风荷载及海浪荷载等随时间变化荷载作用下的响应。
对于求解结构动力问题的方法可参考有关书籍。