▶4.1.2 4结点四面体（一次单元）
如图4.3所示为4结点四面体单元，具有12个自由度。
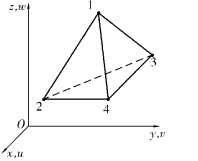
图4.3 4结点四面体单元
单元结点位移列阵为
式中
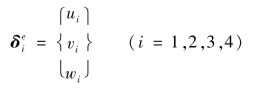
单元结点力列阵为：
式中
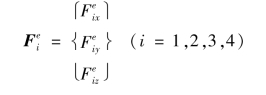
（1）位移模式
与平面问题类似，按照3.1节中单元位移模式选择规则，位移多项式选项可以参照图4.4所示三维Pascal三角锥选取。
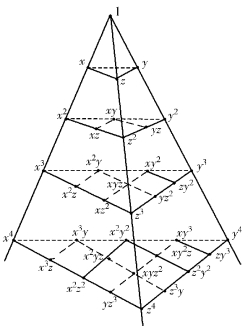
图4.4 三维Pascal三角锥
由于四面体沿每条边只有两个结点，所以，对于协调的位移场，位移函数u，v，w必须沿每一条边是线性函数。因此，选择完全一次多项式作为其位移模式：
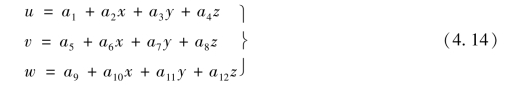
显然，位移模式已满足完备性要求。由式（4.14）可以看出，单元位移函数在边界面上为一平面方程，即在变形过程中该边界面始终保持为平面。这一平面方程能够由该边界面的4个结点唯一确定，因此满足协调性要求，该单元为完备协调单元。
（2）位移插值函数
单元位移插值函数为
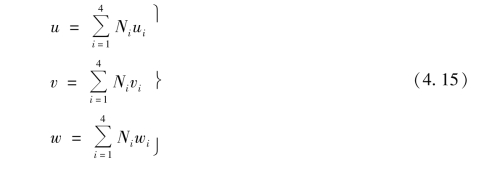
记为矩阵表达式
式（4.15）中，形函数Ni则采用第3章中相似的方法得到，不同之处在于平面问题采用划线方法，而三维问题采用划面法。
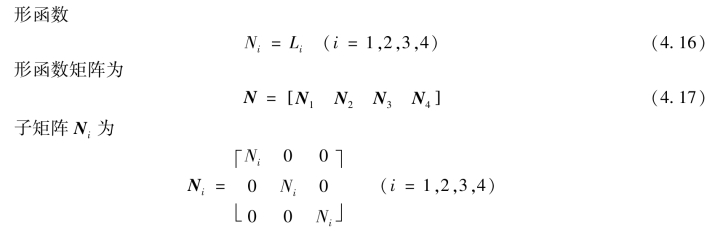
（3）应力与应变
将式（4.16）代入几何方程（1.7）和式（1.8），得到
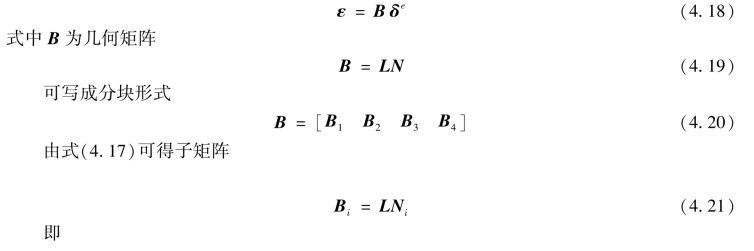
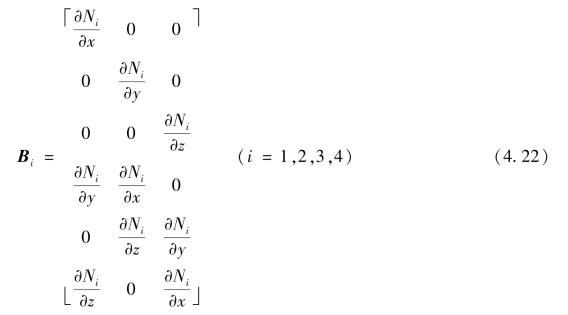
将式（4.4）、式（4.16）代入方程（4.22），可得
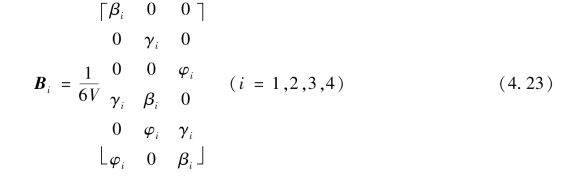
由于式（4.23）中的βi，γi，φi均由结点的坐标值确定，因此，几何矩阵B为常数矩阵。
将式（4.18）代入物理方程（1.16）可得
式中，弹性矩阵D由式（1.17）给出。
（4）单元刚度矩阵
根据第2.2.5节讨论，单元刚度矩阵一般可表达为
对于4结点四面体单元，矩阵B和D都是常数阵，所以方程（4.25）可简化为
式中 V——单元的体积。
（5）等效结点荷载
设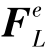
为单元等效结点荷载
根据由第2.2.6节讨论，单元等效结点荷载参照式（2.40）得出
式中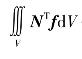 
——体力产生的单元等效结点荷载；
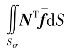——面力产生的单元等效结点荷载。
例如，对于任意4结点四面体单元，其比重为ρg。体力可表示为
将式（4.20）式代入式（4.28），有
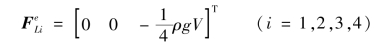
这表明，单元等效结点荷载将体力合力平均分配在4个结点上，即：
此时等效原则符合平行力法法则。
考虑均匀压力p情况，若压力作用在如图4.5所示单元的结点123的表面上，合成的结点荷载为：
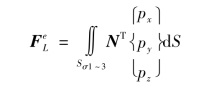
式中 px，py，pz——分别是p的x，y，z分量。
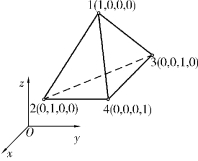
图4.5 4结点四面体单元
简化并积分上式可得到：
式中 S123——与结点123相关的表面面积。