附　录

附　录

附录A　插值函数

从某种角度可以认为，有限元法的核心思想之一就是设定待求函数以有限的待定结点参数在其分块定义域上（有限）进行插值表示，以此来逼近待求函数。学习函数插值的概念以及相关方法对理解和推导有限元是十分重要的。

▶A.1　插值函数

设y=y（x）在区间[a，b]上有定义，且已知在点a≤x1≤x2≤…≤xn+1≤b上的值y1，y2，…，yn+1，若存在函数I（x），使得

则称I（x）为y（x）的插值函数，点x1，x2，…，xn+1称为插值结点，区间[a，b]称为插值区间。

从几何上看，插值法就是求曲线y=I（x），使其通过给定的n+1个点（xi，yi），（i=1，…，n+1），并用它近似已知曲线y=y（x），如图A.1所示。

通常，有n+1个不同插值点的插值函数可以改写成为如下形式：

称Ni（x）为点xi对应的插值基函数。

插值基函数应该具有以下性质：

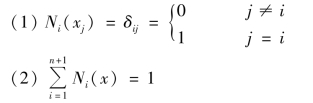
（3）Ni（x）与I（x）函数形式是相同的。特别地，若I（x）是最高次数为n的代数多项式，则Ni（x）也是最高次数为n的代数多项式。

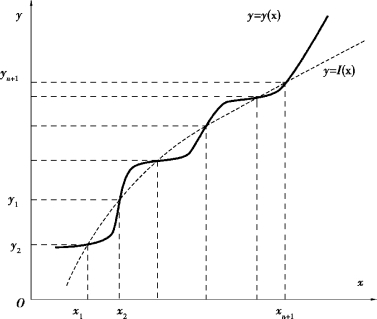
图A.1　函数的插值近似

▶A.2　多项式插值函数

I（x）的形式可能是多种多样，常见的即为多项式函数。

若I（x）的最高次数为n的代数多项式，则I（x）=a0+a1x+…+anxn（其中ai为实数），则称I（x）为插值多项式。这种插值称为代数插值。

拉格朗日插值表示为

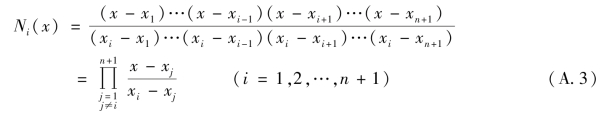
显然，拉格朗日插值多项式满足上述插值基函数应该具有的性质。

▶A.3　分段线性插值函数

在代数插值中，为了提高插值多项式对函数的逼近程度，可以采用增加结点数以提高多项式次数的方法，但这样做往往不能达到预想的结果。直观上容易想象，如果不用多项式曲线，而是将曲线上两个相邻的点用线段连接起来（图A.2），这样得到的折线必定能较好地近似原函数曲线。而且，只要y=y（x）连续，结点越密，逼近程度越好。由此得到启发，为了提高精度，在加密结点时，可以把原区间分成若干段，分段用多项式逼近待定函数，这就是分段插值的思想。用折线近似曲线，相当于分段用线性插值，称为分段性插值。

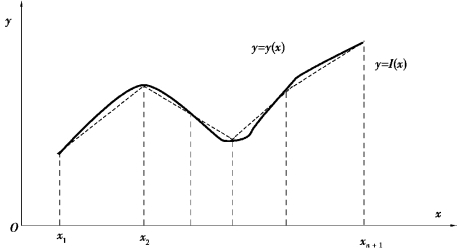
图A.2　函数的分段线性插值

在区间[a，b]上给定n+1个结点，a≤x1≤x2≤…≤xn+1≤b，以及结点上的函数值yi=y（xi）（i=1，2，…，n+1），设插值函数I（x），使

(1)I(xi)=yi(i=1,2,…,n+1);

（2）在每个小区间[xi，xi+1]（i=1，2，…，n+1）上I（x）是线性函数。

则I（x）为区间[a，b]上关于数据（xi，yi）（i=1，2，…，n+1）的分段线性插值，如图A.2所示。

由拉格朗日线性插值公式，容易写出I（x）的分段表达式为

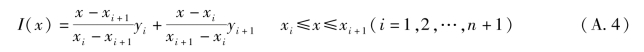
也可以通过改造基函数的方法来求I（x）。

首先构造一组基函数Ni（x）（i=1，2，…，n+1），每个Ni（x）满足

(1)

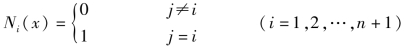
（2）Ni（x）在每个小区间[xi，xi+1]（i=1，2，…，n）上线性函数。

这组函数称为分段线性插值基函数，如图A.3所示。

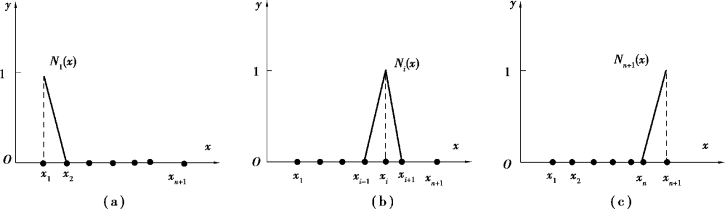
图A.3　分段线性插值的基函数

由图A.3可直接写出Ni（x）的表达式如

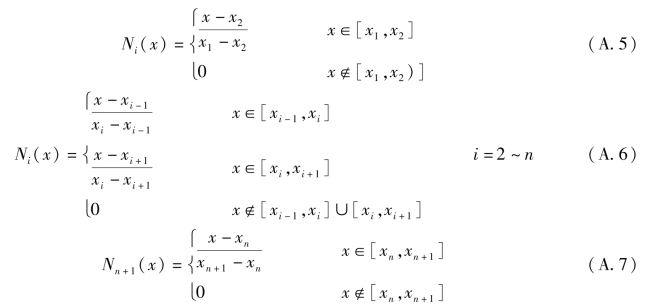
分段线性插值简单易行。可以证明，当结点加密时，分段线性插值的误差变小，收敛性有保证。另一方面，分段线性插值中，每个小区上的插值函数只依赖于本段的结点值，因而每个结点只影响到结点临近的一两个小区间，计算过程中数据误差基本上不扩大，从而保证了结点数增加时插值过程的稳定性。但分段线性插值函数仅在[a，b]上连续，一般来说，在结点处插值函数不可微，这就不能满足有些工程技术问题的光滑度要求。

附录B　变分及能量原理

▶B.1　变分法简介

B.1.1　函数的变分

如果对于变量x在某一变域上的每一个值，变量y有一个值和它对应，则变量y称为变量x的函数，记为

如果由于自变量x有微小增量dx，函数y也有对应的微小增量dy，则增量dy称为函数y的微分，而

其中y＇（x）为y对于x的导数。图B.1中曲线AB表示y与x的函数关系并给出微分dy。

现在，假想函数y（x）的形式发生改变而成为新函数Y（x）。如果对应于x的一个定值，y具有微小的增量

则增量δy称为函数y（x）的变分。显然，δy一般也是x的函数。在图B.1中，用CD表示相应于新函数Y（x）的曲线，并示出变分δy。

例如，假定AB表示某个梁的一段挠度曲线（图B.1），而y是梁截面的真实位移，则CD可以表示该梁发生虚位移以后的挠度曲线，而虚位移δy就是真实位移y（x）的变分。

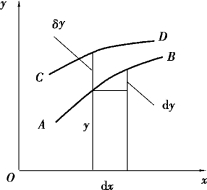
图B.1

当y有变分δy时，导数y＇一般也将有变分δ（y＇），它等于新函数的导数与原函数的导数这两者之差，即

但由式（B.1）有

于是可见有关系式δ（y＇）=（δy）＇，或

这就是说，导数的变分等于变分的导数，因此，微分的运算和变分的运算可以交换次序。

B.1.2　泛函及其变分

如果对于某一类函数y（x）中的每一个函数y（x），变量I有一个值和它对应，则变量I称为依赖于函数y（x）的泛函，记为

简言之，泛函就是函数的函数。

例如，设xy面内有给定的两点A和B（图B.2），则连接这两点的任一曲线的长度为

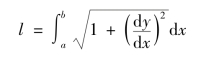
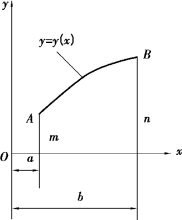
图B.2

显然长度l依赖于曲线的形状，也就是依赖于函数y（x）的形式。因此，长度l就是函数y（x）的泛函。

在较一般的情况下，常见的泛函具有如下的形式：

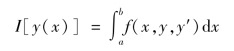
或者简写为

其中的被积函数f（x，y，y＇）是x的复合函数。

首先来考察函数f（x，y，y＇）。当函数y（x）具有变分δy时，导函数y＇也将随着具有变分δy＇。这时，按照泰勒级数展开法则，函数f的增量可以写成

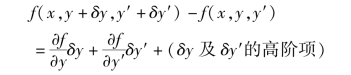
上式等号右边的前两项（关于δy和δy＇的线性项）是函数f的增量的主部，定义为函数f的变分（一阶变分），表示为

进一步考察式（B.4）所示的泛函I。当泛函y（x）及导函数y＇（x）分别具有变分δy及δy＇时，泛函I的增量显然为

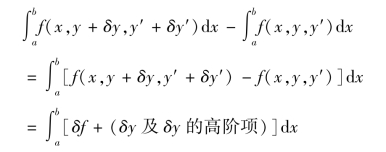
同样，泛函I的一阶变分为

将式（B.5）代入，即得泛函的一阶变分的表达式

由式（B.4）及式（B.6），可见有关系式

这就是说，只要积分的上下限保持不变，变分的运算与定积分的运算可以交换次序。

B.1.3　泛函的极值问题——变分问题

如果函数y（x）在x=x0的临近任一点上的值都不大于或都不小于y（x0），也就是

或

则称函数y（x）在x=x0处达到极大值或极小值，而必要的极值条件为dy/dx=0或dy=0。

对于式（B.2）所示形式的泛函I[y（x）]，也可以通过分析而得出相似的结论如下：如果泛函I[y（x）]在y=y0（x）的临近任意一条曲线上的值都大于或等不小于I[y0（x）]，也就是一阶变分

或

则称泛函I[y（x）]在曲线y=y0（x）上达到极大值或极小值，而泛函极值的必要条件为一阶变分

相应的曲线y=y0（x）称为泛函I[y（x）]的极值曲线。关于泛函I为极值的充分条件是：如果二阶变分δ2I≥0，则I为极小值；如果δ2I≤0，则I为极大值。在一般的泛函极值问题中，只需考虑必要条件就可以了。

凡是有关泛函极值的问题，都称为变分问题，而变分法主要就是研究如何求泛函极值的方法。

下面来讨论这样一个典型的变分问题：设图B.2中y=y（x）所示的曲线被指定通过A，B两点，也就是y（x）具有边界条件

试用泛函I=的极值条件求出函数y（x）。

首先来导出这一变分问题中的极值条件δI=0的具体形式。在变分δf的表达式（B.7）中，右边的第二部分是

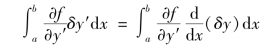
进行分部积分，得

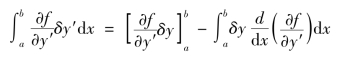
但是，按照边界条件式（B.10），在x=a及x=b处，y不变，因而有δy=0，可见

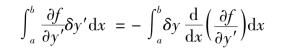
代入式（B.7）的右边，得出

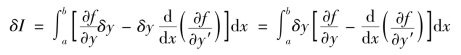
于是，根据δy的任意性，由δI=0得到极值条件

由此可以得出函数y（x）的微分方程，而这一微分方程的解答将给出函数y（x）。

注意：在式（B.11）中，偏导数只表示x，y，y＇三者互不依赖时的运算，而在的运算中，必须考虑y及y＇均为x的函数。

作为简例，试求图B.2中AB曲线为最短时的函数y（x）。在这里，有

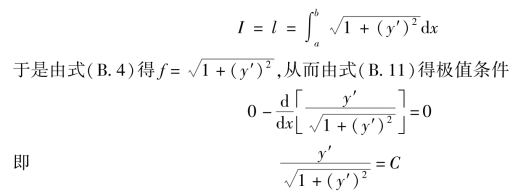
其中C是任意常数。求解这一方程，得y＇=C1，从而有

可见最短曲线为一直线。任意常数C1及C2可由边界条件式（B.10）求得。

▶B.2　弹性理论的能量变分原理

B.2.1　弹性体的总势能

弹性力学变分法中所研究的泛函，就是弹性体的能量，如形变势能、外力势能等。本章介绍变分法中按位移求解的方法，其中取位移为基本未知函数。

在单向受力状态下，弹性体在某一个方向（例如x方向）受有均匀的正应力σx，相应的线应变为εx。若能量守恒，在弹性体在变形过程应力σx所做的功全部转化为弹性体的形变势能。

变形过程中，应力分量σx及其相应的形变的分量εx服从胡克定律，即两者之间成线性关系（图B.3），因此

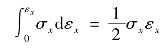
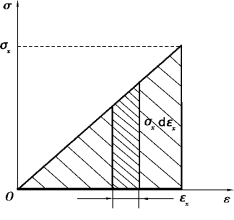
图B.3

设弹性体形变势能为U，单位体积中具有的形变势能为U1，称作形变势能密度，则

对于一般弹性体受有全部6个应力分量σx，σy，σz，τxy，τyz，τzx，由小变形假定，形变势能与弹性体的受力的次序无关，而完全确定于应力与形变的最终大小。形变势能密度为各应力分量在相应应变所做的功之和，从而得到弹性体的形变势能密度

在平面问题中，τyz=0，τzx=0。在平面应力中还有σz=0；在平面应变问题中，还有εz=0。因此，在两种平面问题中，弹性体的形变势能密度的表达式都简化为

为了简便，在z方向取单位长度，平面域A内的形变势能

利用平面应力问题的物理方程

代入式（b），得

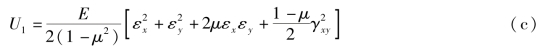
将式（c）分别对εx，εy，γxy求导，参照式（b），有

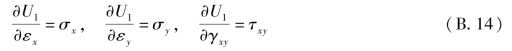
上式表明：弹性体每单位体积中的形变势能对于任一形变分量的改变率，就等于相应的应力分量。

形变势能还可以用位移分量表示。为此，只需将几何方程式

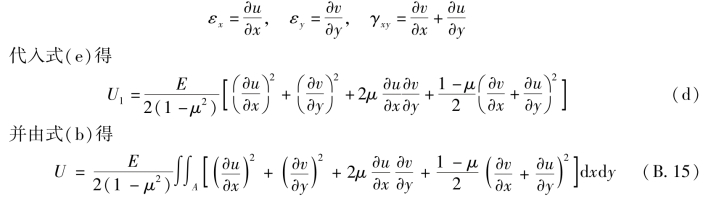
在式（B.15）中，只需将E换为，将μ换为，就得出平面应变问题中相应公式。

由式（B.15）和式（f）可见，形变势能是形变分量或位移函数的二次泛函。

若弹性体受体力和面力作用，平面区域A内的体力分量fx，fy；sσ边界上的面力分量为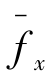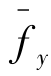，，则外力在相应位移上所做的功称为外力功

由于变形过程中，外力做功，降低了外力势能，因此在发生实际位移时，弹性体的外力势能是

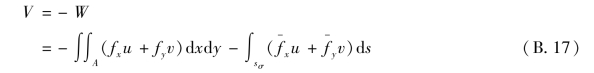
弹性体的形变势能与外力势能之和，即为弹性体的总势能Πs：

B.2.2　位移变分方程

设有平面问题中的任一单位厚度的弹性体在一定的外力作用下处于平衡状态。令u，v为该弹性体中实际存在的位移分量，它们满足用位移分量表示的平衡微分方程，并满足位移边界条件以及用位移分量表示的应力边界条件。现在假设这些位移分量发生了位移边界条件所容许的微小改变，即所谓虚位移或位移变分δu，δv，这时，弹性体从实际位移状态进入邻近的所谓虚位移状态：

例如，图B.4中的梁在外力作用下的实际位移为v，它满足平衡微分方程、位移边界条件和应力边界条件。假设在实际位移状态附近发生了约束条件（位移边界条件）容许的虚位移δv，则梁进入邻近的虚位移状态v＇=v+δv。由于虚位移时满足约束条件的，因此在边界的约束处，即点A和点B，δv=0。

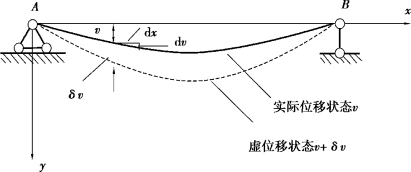
图B.4　位移变分

现在来考察，由于弹性体发生了虚位移，所引起的外力势能和形变势能的改变。

由于位移的变分δv，δv引起的外力功的变分δW（即外力虚功）和外力势能的变分δV为

由于位移的变分，引起应变的变分（虚应变）为

从而引起形变势能的变分为

假定弹性体能量守恒，形变势能的增加应当等于外力的势能的减少，也就等于外力所做的功，即外力虚功，于是得

将式（B.17）代入上式，得

式（B.21）即为位移变分方程。它表示：在实际平衡状态发生位移的变分时，所引起的形变势能的变分，等于外力功的变分。从位移变分方程（B.21）出发，可以导出最小势能原理。

▶B.2.3　最小势能原理

将式（B.21）写成

上式的第二项中外力是真实作用力，可以将变分记号δ提到积分号前面。

同理，由式（B.19）可得

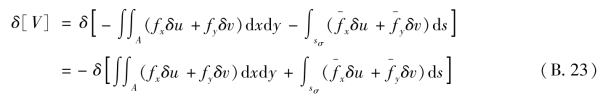
将式（B.23）代入式（B.22），整理可得

式（B.24）表明，实际存在的位移应使总势能的变分为零。这就推导出这样一个定理：在给定的外力作用下，在满足位移边界条件的所有可能的位移函数中，真实的位移函数应使总势能称为极值。

可以证明，真实位移不仅使势能为驻值，而且使势能为极小值。因此，上述原理称为最小势能原理。

设u是真实位移，u+Δu是与真实位移临近的任意可能位移（显然，位移差Δu是齐次可能位移），则

证：根据势能定义式（B.35），有

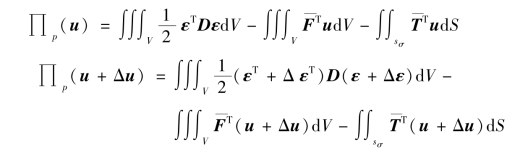
以上两式相减，得

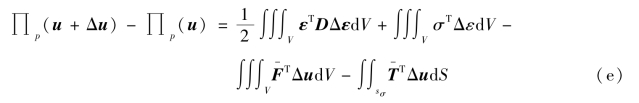
由于σ是真实应力，满足静力方程。而Δu是齐次可能位移，因此虚位移方程成立。仿照式（B.31），有

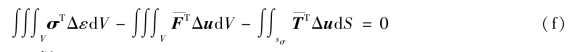
将式（b）代入式（a），得

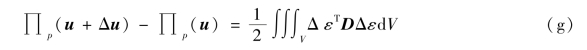
上式右边是应变Δε相应的应变能，不可能是负值。因此，式（B.42）成立。

▶B.2.4　虚功方程

应用位移变分方程，还可以导出另一个重要方程，即弹性力学的虚功方程。为此，将δU用式（B.20）表示，再代入位移变分方程（B.21），得到虚功方程

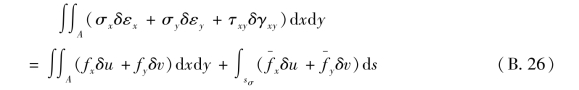
这就是虚功方程。它表示：如果虚位移发生之前，弹性体处于平衡状态，那么，在虚位移过程中，外力在虚位移上所做的虚功就等于应力在虚应变上所做的虚功。

从以上的讨论可知，位移变分方程（B.21）、最小势能原理（B.24）以及虚功方程（B.26）三者是等价的。它们都是弹性体从实际平衡发生虚位移时，能量守恒定理的具体应用，只是表达方式有所不同。进一步的研究表明，还可以从位移变分方程（或极小势能原理，或虚功方程）导出平衡微分方程和应力边界条件。这就证明：位移变分方程（或极小势能原理，或虚功方程）等价于平衡微分方程和应力边界条件，或者说，可以代替平衡微分方程和应力边界条件。

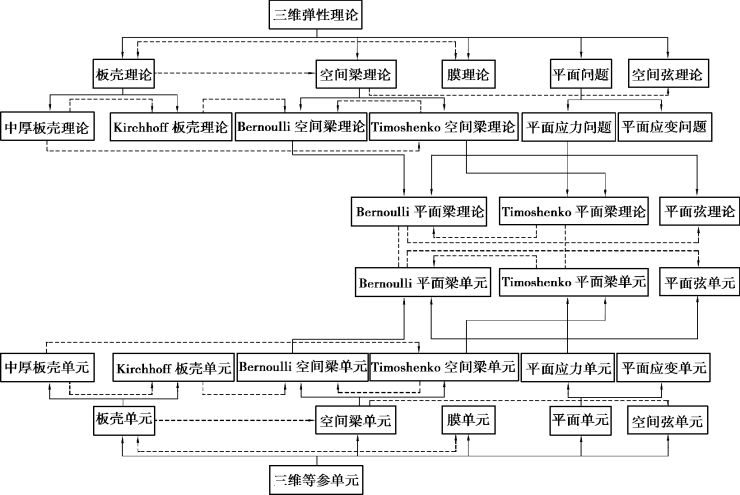
附录C　三维实体单元和退化单元系列关系