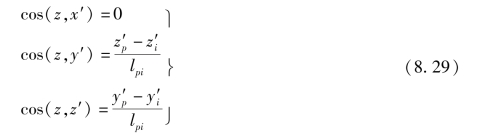▶8.2.3 局部坐标的方向余弦
如上节所述，为了建立结点平衡方程，需要用到各单元局部坐标的方向余弦矩阵λ，见式（8.11）。
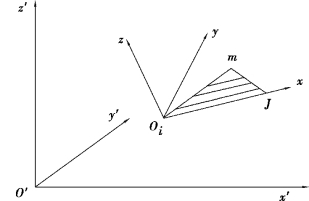
图8.7 三角形单元的局部坐标
如图8.7所示的三角形单元ijm，3个结点的整体坐标为
。今取结点i为局部坐标的原点，ij边为x轴，y轴在单元平面内并垂直于ij边，z轴垂直于单元平面。如果把ij边作为一个矢量Vij，可用该矢量在整体坐标系中的3个分量表示为
其中
用该矢量的长度除它的3个分量，即得到该矢量的方向余弦，也就是局部坐标x轴在整体坐标系中的方向余弦，从而得到一个单位矢量如下：
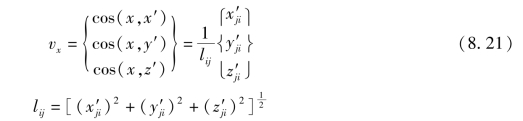
z轴是垂直于三角形平面的，利用2个矢量的矢积垂直于2个矢量所在平面的性质，可得到垂直于三角形平面的矢量Vz如下：
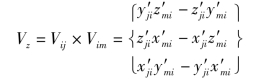
由于矢量Vz的长度等于△ijm面积的2倍，即
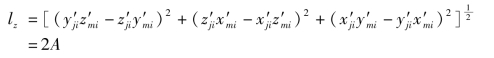
故z轴的方向余弦为
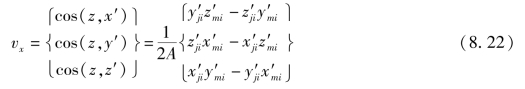
同理可求得y轴的方向余弦，由于y轴垂直于xz平面，因此单位矢量vz和vx的矢积等于y轴方向的单位矢量，即
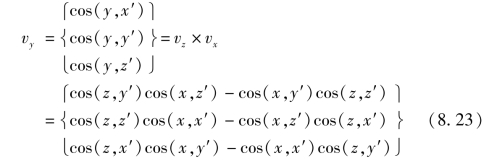
由于vy的长度等于1，所以不必再除以它的长度了。至此，局部坐标的方向余弦矩阵λ的全部元素都求出来了。
在上面的计算中，我们规定局部坐标的x轴沿着单元的ij边，当然这并非唯一的办法。也可采用其他办法来规定局部坐标系。例如，在水坝、冷却塔、油库等壳体计算中，为了便于整理成果，最好把整体坐标系的x＇y＇面放在水平面内，并使局部坐标系的x轴平行于x＇y＇面。局部坐标的z轴仍垂直于三角形平面，故首先可用式（8.22）计算z轴的方向余弦。其次，由于局部坐标的x轴垂直于z＇轴，所以x轴的方向余弦是
由于各个方向余弦的平方之和等于1，故
另外，vx与vz的标乘积应等于零，即
由以上两个方程求解，可以解出cos（x，x＇）和cos（x，y＇），从而可得到vx。求得vx和vz后，再由式（8.23）可求出vy。
对于矩形单元，其应用范围只限于柱面或箱形薄壳，而且壳的边界必须平行或垂直于柱面的母线方向，因此，可以将整体坐标系的x＇轴放在柱面的母线方向，并使各个单元局部坐标系的x轴平行于x＇轴，如图8.8所示。
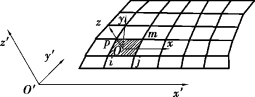
图8.8 矩形单元的局部坐标
显然，x轴的方向余弦是
由于y轴平行于pi边，由结点p和i在整体坐标系中的坐标，可计算y轴的方向余弦如下：
其中lpi是pi边的长度，即
同样，可求得z轴的方向余弦如下：
