▶2.3.4 位移解的下限性质
以位移为基本未知量，并基于最小势能原理建立的有限元称为位移元。通过系统总势能的变分过程，可以分析位移元的近似解与精确解偏离的下限性质。
将式（2.61）代入式（2.59）得到
在平衡条件下，系统总势能等于负的应变能。
在有限元解中，由于假定的近似位移模式一般来说总是与精确解有差别，根据最小势能原理，其真实解使总势能取最小值。因此有限元解得到的系统总势能总会比真实解的总势能要大。
将有限元解的总势能、应变能、刚度矩阵和结点位移分别用
表示，相应精确解的有关量用Πp，U，K，δ表示。
由于
，由式（k）有
，即
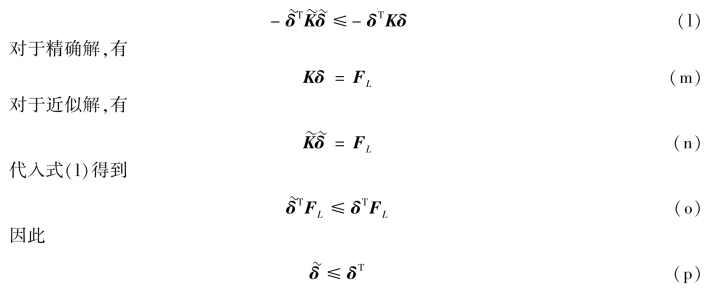
式（p）表明，位移有限元得到的位移解总体上不大于精确解，即解具有下限性质。
位移解下限的性质可以做如下解释：单元原是连续体的一部分，具有无限多个自由度。在假定了单元的位移函数后，自由度限制为只有以结点位移表示的有限自由度，即位移函数对单元的变形进行了约束和限制，使单元的刚度较实际连续体加强了，因此连续体的整体刚度随之增加，离散后的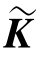
较实际的K为大，因此求得的位移近似解总体上（而不是每一点）将小于精确解。
而以应力作为基本未知量，按照最小余能原理求解时，单元的计算刚度小于实际刚度，因而位移解将大于或等于精确解，具有上限性质。对此可解释为：按照最小余能原理求解时，在相邻单元的公共边界上，应力是平衡的，但位移是不连续的，计算模型的变形能力增加了，比真实物体更加柔软，因而具有上限性质。
当采用杂交单元求解时，不能肯定所得到的位移近似解是大于还是小于精确解。大体说来，其数值是介于按照最小势能原理求解与按照最小余能原理求解所得到的两种结果之间。
对于工程应用来说，重要的是应弄清楚在合理单元划分的典型问题中所能达到精度的阶次。在任何情况下，可以通过比较已知的精确解或者通过两种或多种更细的单元划分来研究误差的收敛性。
随着经验的积累，对于一个指定问题，工程师能够事先估计出所使用的单元划分可得到近似值的阶次。对于应力计算误差和精确解的评估可参考其他文献。