5.3 8结点四边形平面等参单元
对于图5.6（b）中为整体坐标x，y中的任意8结点曲边四边形单元，建立一个与此单元对应的边长为2的8结点正立方体单元，并在其形心位置建立局部坐标系ξ，η，如图5.6（a）所示。将此单元作为母单元。
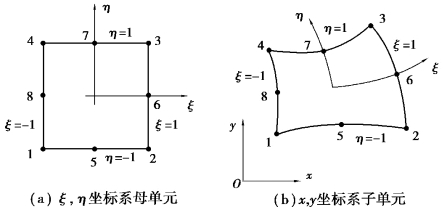
图5.6 8结点四边形单元
（1）母单元位移模式
参照第3.3.2节分析，在局部坐标系中，单元位移模式可取为
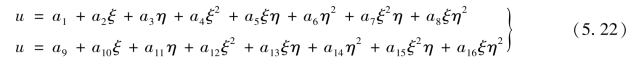
显然，该单元为协调元。单元位移插值函数为
式中，Ni（ξ，η）为形函数，参照式（3.52），可取为
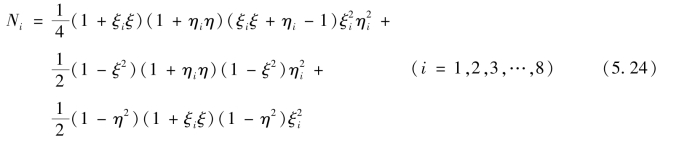
（2）等参坐标变换
如图5.6（b）所示为整体坐标系的任意曲边四边形单元，同样设置8个结点，对两种坐标系采用下式进行变换：
式中，Ni（ξ，η）为位移插值函数中的形函数，由式（5.24）表示。
由式（5.25）可以看出，通过坐标变换，图5.6（b）整体坐标x，y中的曲边四边形映射为图5.6（a）局部坐标ξ，η中的正方形单元。曲边四边形的4个角点1，2，3，4与正方形的4个角点1，2，3，4一一对应，曲边四边形的4个边中点5，6，7，8与正方形的4个边中点5，6，7，8一一对应，曲边四边形中相应的点（x，y）与正方形中任意点（ξ，η）一一对应。
由位移函数（5.22）知，曲边四边形的每一条边界均为二次函数，可由该边界的3个结点唯一确定。因此，曲边四边形单元相应的二次曲线边界映射为正方形单元每一条直线边界，从而，图5.3（b）中的曲边四边形单元一一对应的映射为图5.6（a）中所示的正方形母单元。该曲边四边形单元称作子单元。
对于实际问题，可将弹性体划分为若干个8结点曲边四边形单元。由于各单元边界为二次曲线，因此，整个弹性体的边界近似地用若干段二次曲线来拟合。如此一来，与前述“以折代曲”的方法相比，能更好地适应各类复杂的边界。
（3）应变与应力
将式（5.23）代入平面问题的几何方程，得到单元的应变
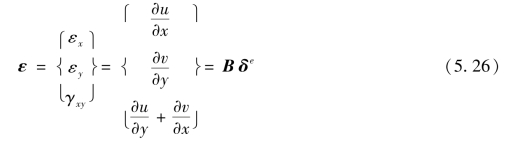
式中，B为几何矩阵
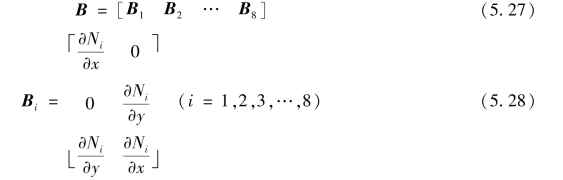
由于形函数Ni为局部坐标ξ，η的函数，由上一节分析，参照式（5.12）可知
由式（5.25）可得整体坐标x，y对自然坐标的ξ，η偏导数
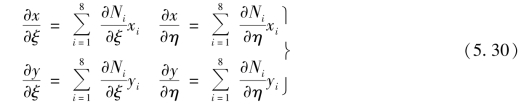
其中，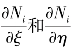
由式（5.2）求导可得
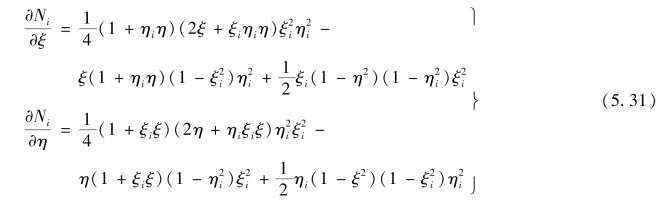
将式（5.7）代入平面问题的物理方程，得到单元的应力
将上式中的应力矩阵S写成分块形式
对于平面应力问题，各子块
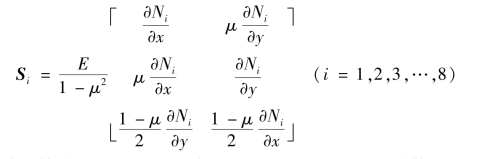
单元刚度矩阵和单元等效结点荷载可分别由式（5.18）和式（5.20）计算。
表5.1中给出了采用常应变三角形单元、矩形单元以及等参数单元计算如图5.7所示平面悬臂梁在两种荷载作用下的结果。可见，用1排矩形单元或2排三角形单元计算的误差还是相当大的，使用1排8结点等参数单元就可得到满意的计算结果。
表5.1 采用不同单元计算平面悬臂梁
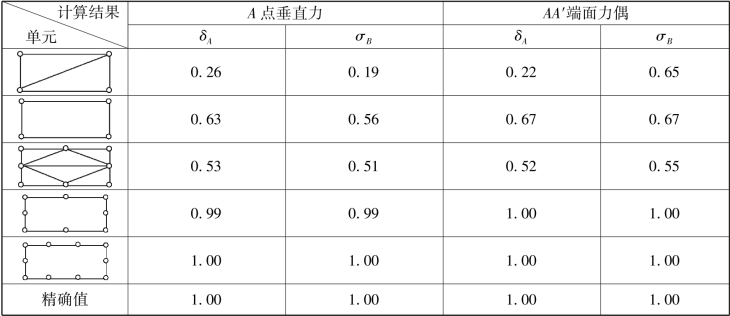
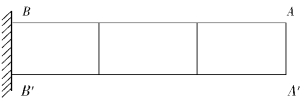
图5.7 平面悬臂梁
（4）单元收敛性讨论
等参元是有限单元法中的一类单元，亦必须满足单元的收敛条件。下面以8结点四边形等参元为例，具体讨论等参数单元的完备性和协调性。
首先讨论单元的完备性。
由第2.2.7节讨论中可知，在平面问题中，对应于刚体位移和常应变状态的位移可以写成完全一次多项式
设等参数单元的8个结点位移包含式（5.21），于是
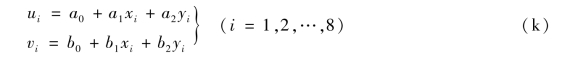
单元内任一点的位移为
其中，Ni（ξ，η）由式（5.22）表示。将式（m）代入式（j），得
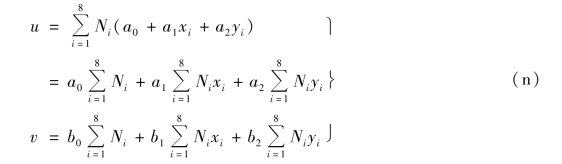
由坐标转换关系式（5.25），可得
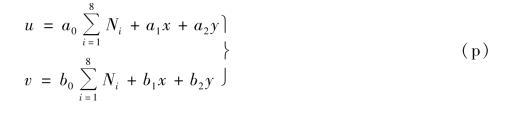
若
=1，则式（p）成为式（j）的形式，即单元内的位移是刚体位移或对应于常应变的位移，单元具有完备性。
如图5.8所示，xy为等参元整体坐标
为另一个整体坐标系，则有
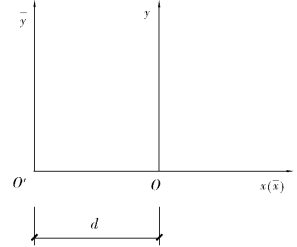
图5.8
若以
为等参元的整体坐标系，同样有
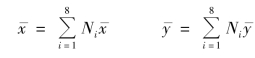
代入式（5.25），得
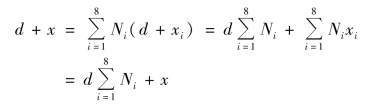
故
，命题得证。下面，讨论8结点等参元的协调性。
由于式（5.24）中形函数Ni（ξ，η）为连续函数（多项式），所以满足位移在单元内的连续性。在相邻单元的公共边界，由于单元位移都是二次曲线，该曲线可以由边界上的3个结点坐标所唯一确定，所以相邻单元的公共边界上是同一条二次曲线，故满足单元的协调性要求。
综上，平面问题8结点曲线四边形等参数单元是完备协调单元，其解答必定收敛。