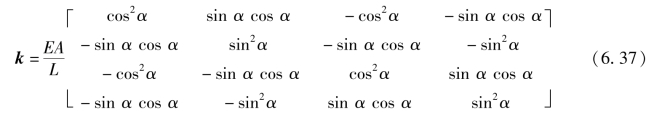▶6.2.1 平面杆单元
杆单元可以处在平面内（比如Oxy平面内）的任意方位，既可以与坐标轴平行，也可以与坐标轴不平行，称处在平面内任意方位的杆单元为平面杆单元。如图6.2所示为一个具有两个结点的杆单元。取两个直角坐标系：Oxy（总体坐标系）和Ox＇y＇（局部坐标系），两个坐标系之间的夹角为α，杆单元的轴线与局部坐标系的x＇轴重合。
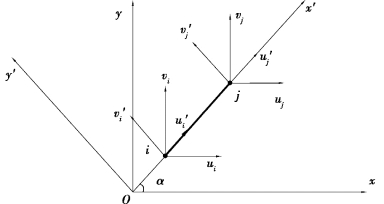
图6.2 平面杆单元
假设平面杆单元在局部坐标系下的结点位移和结点力分别为
而在总体坐标系下的结点位移和结点力分别为
现将第6.1节建立的一维杆单元的刚度矩阵式（6.22）与图6.2中的杆单元相对应，即把图6.1中的坐标系看作图6.1中的局部坐标系，对于局部坐标系来说，式（6.22）中刚度矩阵的元素表示了局部结点位移
与局部坐标系中的结点力
之间的关系，即
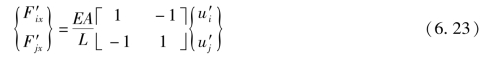
由于杆单元只能承受轴向力，也只有轴向刚度，如果把与局部坐标y＇方向对应的结点力和结点位移也放入式（6.23），则有
式（6.24）表示的是局部坐标系中的结点力和结点位移之间的关系。注意，刚度矩阵中与局部坐标y＇方向的结点力和节点位移相关的元素都为零，即在局部坐标系中，y＇方向的结点力和结点位移为零，这样式（6.23）和式（6.24）是等价的。
若令
则式（6.24）可写为
为得到总体坐标系中的结点力和结点位移的关系，可以采用如下转换，将局部坐标系下的结点位移（δe）＇和结点力（Fe）＇分别用总体坐标系下的结点位移δe和结点力Fe表示，然后把总体坐标系下的结点位移和结点力表示的（Fe）＇和（δe）＇代入式（6.26），就可以得到总体坐标系下的单元刚度矩阵。
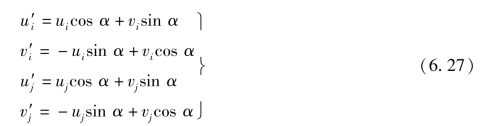
式（6.27）写成矩阵形式，则有
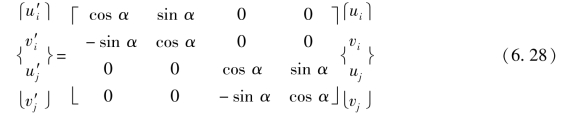
若令
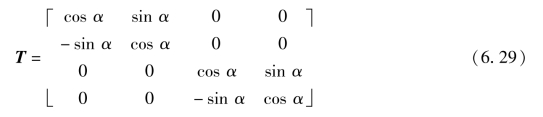
则有
对于局部坐标系下的结点力（Fe）＇和总体坐标下的结点力Fe，同样有与式（6.28）类似的转换关系，即
式（6.36）就是总体坐标系下表示单元结点力和结点位移之间关系的单元刚度方程。由式（6.35）知，对于平面杆单元，可以利用局部坐标系下的单元刚度矩阵k＇，通过坐标转换得到总体坐标系下的单元刚度矩阵。
将式（6.25）和式（6.29）代入式（6.35），可得到单元轴线与整体坐标系x轴的夹角为α的平面杆单元的刚度矩阵为
