▶2.2.4　应力转换矩阵

▶2.2.4　应力转换矩阵

利用几何方程和物理方程可求得单元的应变和应力。

将式（2.14）代入几何方程（1.7）得

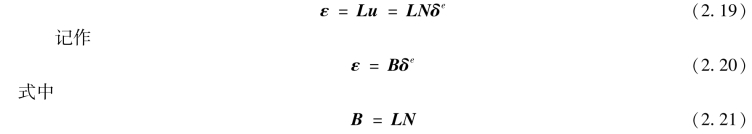
称为几何矩阵。式（2.20）为由结点位移δe表示应变ε的转换式。

对于3结点三角形单元，由式（2.11）、式（2.13）可得

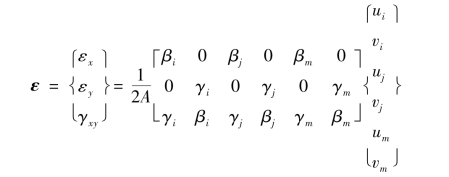
可见，对于3结点三角形单元，B的元素是与单元的几何性质有关的常量，即B为常数阵，因此，3结点三角形单元通常称作常应变单元（CST）。

几何矩阵B可表示为分块形式

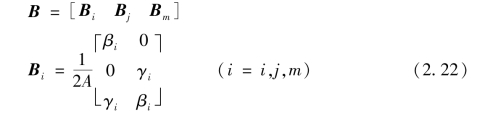
将式（2.19）代入物理方程式（1.16），可得由应变求应力的转换式：

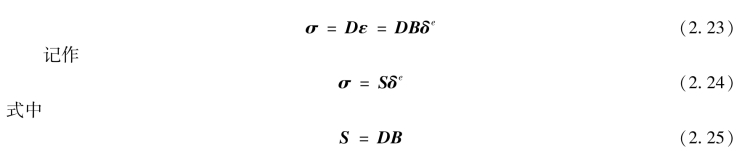
称为应力转换矩阵。

由式（2.23）可见，对于3结点三角形单元，常应变单元内部，其应力也是常数，通常可认为该数值是三角形单元的平均值。因此，单元的应力值在相邻边界处是不连续的。

至此，应力σ、应变ε以及位移u均已用单元基本未知量结点位移δe来表达。

下面利用最小势能原理，建立单元的基本方程。