▶5.6.1　一维高斯积分

▶5.6.1　一维高斯积分

将式（5.62）中第一式的求和展开，有

研究表明，当取n个积分点时，高斯积分具有2n-1阶的精度，即如果被积函数是不高于2n-1次的多项式，则积分结果是精确的。下面通过讨论设置1个和2个积分点的高斯积分，以比较直观的方法，考察如何确定高斯积分点坐标ξi和权系数ωi。有兴趣的读者可参考有关文献。

（1）设置2个积分点

当n=1（即取一个积分点）时，如果f（ξ）是一次多项式，则式（5.63）为精确积分，这就要求误差Rn等于零，即

令f（ξ）为一次多项式，即

将式（b）代入式（a），则要求

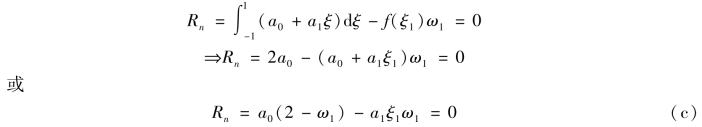
从式（c）可以看到，如果

则误差为零。所以，一点高斯积分的积分点坐标和权系数应取为

因此，如果是一次多项式，则高斯积分为精确积分，即

（2）设置1个积分点

当n=2（即取2个积分点）时，如果f（ξ）是不高于三次的多项式，则式（5.63）为精确积分，这就要求误差Rn等于零，即

令f（ξ）为任意三次多项式，即

将式（e）代入式（d），则要求

完成上式积分，并令误差等于零，则得到

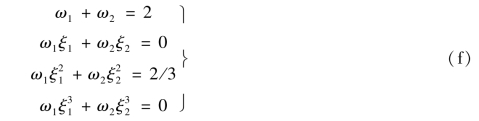
解之，可得两点高斯积分的积分点坐标和权系数为

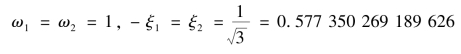
此时，高斯积分公式为

采用同样分析方法可以确定取更多积分时所对应的积分点坐标和加权系数。于是，当f（ξ）是不高于2n-1次的多项式时，采用n个积分点，则高斯积分结果是精确的。

实际应用中，根据所求问题的精度要求设置高斯积分点的数目，按照式（5.64）进行近似计算

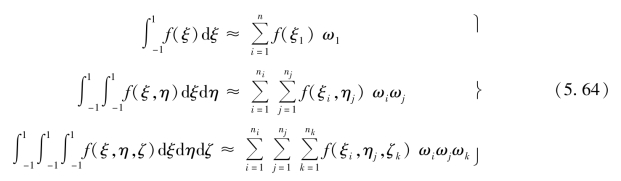
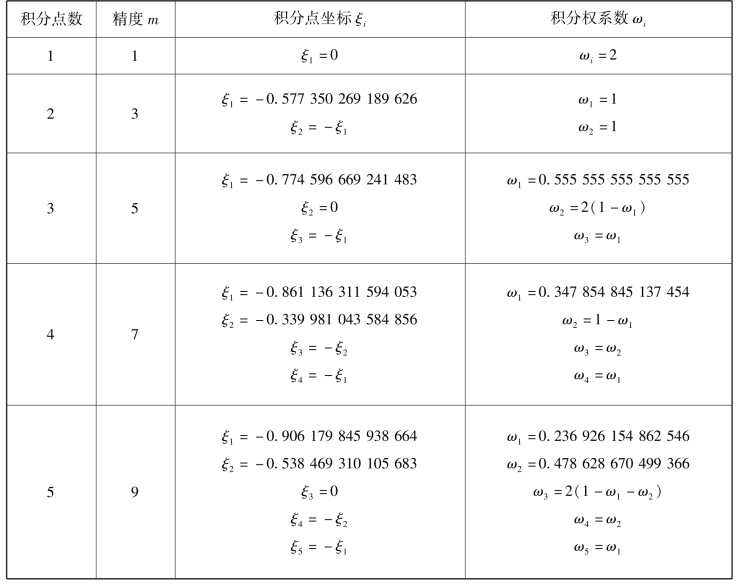
表5.2中列出了在积分域（-1，+1）内，当n=1，2，3，4，5，6时的积分点的坐标和加权系数。

表5.2　Gauss-Legendre数值积分点的坐标和加权系数